9.1.4 Merkpunkte zu Kapitel 9.1: Majoritäten und Minoritäten

	Die einfache Formel für die Ladungsträgerdichte (effektive Zustandsdichten und Boltzmann-Näherung ) in intrinsischen Halbleitern ist ziemlich gut.			ne »    N eff  · exp(– EL – EF kB T  )         nh »    Neff  · exp(– E F– EV kBT  )
		Wir werden deshalb nur noch mit dieser Formel rechnen (bis wir eine noch einfacherer Formel haben werden). Þ
		Für die jetzt vertrauten Löcher ergeben sich (immer mit entsprechendem Vorzeichenwechsel) völlig symmetrische Beziehungen.
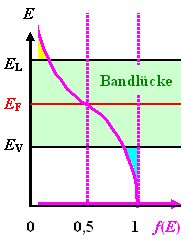
	Die Fermieenergie EF für intrinsische Halbleiter folgt aus n e=nh oder – allgemeiner – aus der notwendigen Ladungsneutralität.			EF  =  EL + EV 2
		Die Fermienergie liegt in der Mitte der Bandlücke.
		Das läßt sich sowohl leicht errechnen, als auch graphisch sofort erkennen: Die "Zwickel" müssen gleich groß sein.
		Der gezeigte Fall, daß die "Zwickel" so weit in die Bänder hineinragen, entspricht der Eigenleitung; sie tritt bei Temperaturen auf, für die 4 kBT ≥ Eg gilt.
	Löcher benehmen sich im wesentlichen wie positiv geladene Elektronen. Ihr Beitrag zur Leitfähigkeit ist damit Þ			sh  =  +e · nh · mh       s total  =  se  +  sh »  2s e
		Löchern kann neben einer Dichte und einer pos. Ladung auch eine Beweglicheit mh zugeordnet werden; sie ist ähnlich zu der der Elektronen.
		Während Elektronen, wenn sie können, energetisch tiefer sinken, steigen Löcher aber auf – wie Luftblasen im Wasser!
	Das Massenwirkungsgesetz ergibt sich aus obigen Konzentrationsgleichungen; es ist sehr wichtig!			ne · nh=ni2 Halbleiter Ge Si GaAs Energielücke [eV] 0,661 1,12 1,424 ni(RT) [cm–3] 2·1013 1·1010 2,1·106
		Dabei ist ni=ne=nh die intrinsische Ladungsträgerdichte für ideal-perfekte Halbleiter, bei denen Elektronen- und Löcherkonzentration per definitionem gleich groß sein müssen.
		ni ist eine Materialkonstante, direkt verknüpft mit der Energielücke Eg.
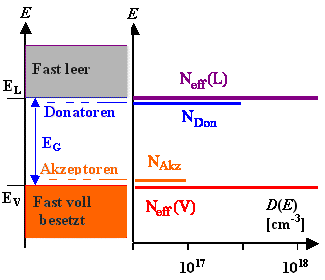
	Dotieren=gezieltes Einbringen von Dotierstoffen (als substitutionelle atomare Fehlstellen) mit Elektronenzuständen in der Energielücke dicht an den Bandkanten.
		Donatoren (in Si entweder P oder As) haben einen am Atom lokalisierten besetzten Zustand dicht unterhalb der Leitungsbandkante. Das dort "sitzende" Elektron kann leicht ins Leitungsband springen und ist dann frei beweglich. Zurück bleibt ein ortsfestes positiv geladenes P+ -Ion.
		Akzeptoren (in Si immer B) haben einen am Atom lokalisierten unbesetzten Zustand für Elektronen dicht oberhalb der Valenzbandkante. Elektronen aus dem Valenzband können leicht auf diesen Zustand springen und ihn besetzen. Wir haben insgesamt ein frei bewegliches Loch im Valenzband und ein negativ geladenes ortsfestes B– -Ion .
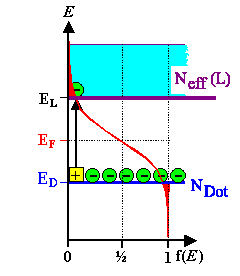
	Entscheidend ist, wie immer, die Lage der Fermienergie.
		Bei kleinen T kommen alle Elektronen in L von den Dotierniveaus; EF muss zwischen Donatorniveau ED und dem Leitungsband sitzen.
		Das gilt auch noch bei höheren Temperaturen: E F ist in der Nähe des Dotierniveaus.
		Wir haben mit Dotieren sehr viel mehr Ladungsträger einer Sorte als im undotierten intrinsischen Halbleiter, bei dem beide Dichten gleichgroß sind.
		Die Dichte nMaj der Majoritätsladungsträger ist in Si bei RT guter Näherung identisch zur Dichte der Dotieratome NDot .		n Maj  =  N Dot       n Min( T)  =  ni2(T) NDot
		Die Dichte der Minoritätsladungsträger nMin folgt aus dem Massenwirkungsgesetz .
		Donatoren: P und As    Þ  n-Si Þ   Majoritäten sind Elektronen im Leitungsband. Minoritäten sind Löcher im Valenzband.
		Akzeptoren: Nur B   Þ   p-Si Þ   Majoritäten sind Löcher im Valenzband. Minoritäten sind Elektronen im Leitungsband.
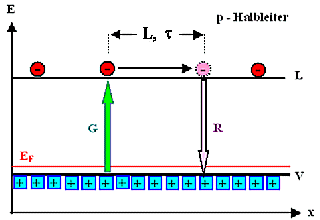
	Ladungsträger in den Bändern werden durch Generation erzeugt (immer thermisch, bei Beleuchtung auch durch Licht), laufen etwa eine Diffusionslänge weit per "random walk" durch den Kristall, und verschwinden wieder durch Rekombination.
		Beide Prozesse werde durch Raten beschrieben; Maßeinheit: s–1 G=Generationsrate R=Rekombinationsrate
		Da im Gleichgewicht die Ladungsträgerdichte konstant ist, muss gelten: G=R sowohl für Minoritäten als auch für Majoritäten.
	Von Interesse ist vor allem die Rekombinationsrate RMin der Minoritäten, da Änderungen der Ladungsträgerdichte bei den Minoritäten sehr viel stärker "durchschlagen"			R =  nMin t L =  (D · t)½ Im Gleichgewicht:         G=R =  nMin t
		Es gilt unmittelbar Þ
		Dabei ist t die Minoritätsladungsträgerlebensdauer (kurz Lebensdauer); leicht zu visualisieren und mit der Diffusionslänge Lgekoppelt durch Þ
		Daraus folgt die dritte wichtige Halbleitergleichung Þ
	Es gibt bezüglich der Rekombination zwei Arten von Halbleitern.			Direkte Halbleiter: L und t sind klein (ungefähr ns / µm) Prominente Vertreter: GaAs, InP, GaN. Indirekte Halbleiter: L und t sind groß und stark defektabhängig (ungefähr µs -ms/ 500 µm) Prominente Vertreter: Si, Ge, SiC.
		Direkte Halbeiter: Rekombination ist leicht; die Überschussenergie produziert ein Photon , d.h. es wird Licht mit hn=EG emittiert. Direkte Halbleiter sind die Grundlage für die Optoelektronik
		Indirekte Halbeiter: Rekombination ist schwer; die Überschussenergie produziert Phononen, d.h. es wird Wärme erzeugt. Silizium ist ein indirekter Halbleiter .

© H. Föll (MaWi für ET&IT - Script)