|
Die grundsätzliche Beschreibung von Spannungszuständen mit Hilfe des
Spannungstensors ist vollständig allgemein - wir können immer beliebige Kräfte auf den differentiellen Einheitswürfel
wirken lassen. |
|
 |
Die Beschränkung auf elastische Verformungen
berührt nur das Verformungsgesetz, d.h. die Beziehung zwischen den Tensoren s und e. |
|
 |
Wir können den Spannungstensor also auch für nichtelastische
Verformungen benutzen - für plastische Verformung und Bruch. |
 |
In diesem Kapitel wollen wir einige ganz allgemeine Beziehungen zwischen Verformungsarten
und Spannungstensoren kennen lernen. Dazu müssen wir uns zuerst einige simple Regeln
aufstellen. |
|
 |
1. Wir betrachten jetzt grundsätzlich nur Spannungszustände
im Hauptachsensystem. |
|
 |
Die im vorherigen Unterkapitel gezeigten Spannungszustände
für hochsymmetrische Belastungen sind, bis auf die reine Scherung, schon im Hauptachsensystem - es ist das "natürliche"
KO System. |
|
 |
Der ebenfalls gezeigte Spannungszustand der reinen Scherung muß durch eine Koordinatentransformation
in einen reinen Normalspannungszustand überführt. Wie man das macht ist hier nicht wichtig, aber in einem anderen Modul gezeigt. In dem neuen KO System hat auch der Spannungstensor der
reinen Scherung nur noch die Diagonalelemente s1, s2
und s3. |
|
 |
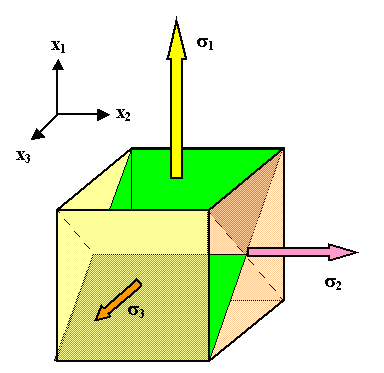
2. Die Koordinatenachsen werden jetzt immer so gewählt, daß
s1 > s2 > s3. |
 |
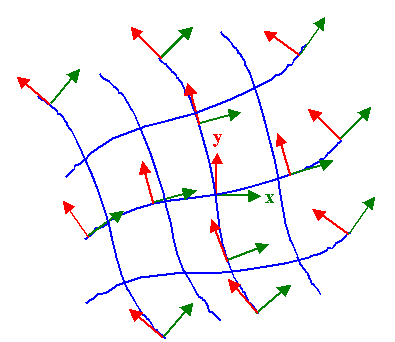
Es ist wichtig sich klar zu machen, daß das Hauptachsensystem an jedem Punkt des unter Spannung stehenden Körpers definiert werden muß, wobei es sich
natürlich in nicht-pathologischen Fällen stetig ändert, wie in einem
beliebigen Beispiel unten gezeigt. |
| |
|
 |
Das Feld der Koordinatensystem-Einheitsvektoren, symbolisiert durch die blauen
Linien, enthält offenbar die wesentliche Information über den Spannungszustand und (bei den üblichen linearen
Materialgesetzen) Dehnungszustand. |
 |
Im jeweiligen Hauptachsensystem gelten zwei Sätze: |
|
 |
Satz 1a: Die maximale Scherspannung die auftreten
kann ist gegeben durch
|
| |
|
|
 |
Satz 1b: Die Ebene mit maximaler Scherspannung
liegt unter 45o zu den Ebenen auf denen s1 und s3
wirkt, wie unten illustriert. |
| |
|
|
 |
Die beiden grünen Ebenen sind die Ebenen maximaler Scherspannung. Zu beachten ist, daß
bei der Wahl des kleinsten s nicht der Betrag zu nehmen
ist - negative s, d.h. Druckspannungen sind kleiner
als positive s, z.B ist – 5 GPa eine kleinere
(Druck)spannung als – 2 GPa oder + 8 GPa. |
 |
Wir werden diesen Satz nicht beweisen; er ist nahezu direkt einsichtig. Wir sind
nun in der Lage, die beiden wirklich wichtigen Sätze zu formulieren: |
|
 |
Satz 2: Die maximal auftretende Scherspannung bestimmt
plastische Verformung. Sie beginnt durch Versetzungsbewegung auf derjenigen Gleitebene, die der Ebene maximaler Scherspannung am nächsten liegt. |
|
 |
Entscheidend ist, ob auf dieser Gleitebene die vorliegenden Scherspannungen eine für
Versetzungsbewegung notwendige kritische Scherspannung tkrit erreichen. |
|
 |
Satz 3: Die maximale Normalspannung, d.h. s1,
ist bestimmend für das Eintreten eines Bruchs. |
|
 |
Sobald s1 > sBruch,
wird die Probe unvermittelt brechen. |
 |
Auch diese Sätze werden wir nicht beweisen, da sie sich aus dem folgenden
fast von alleine ergeben. Wir werden aber jetzt schon einige wichtige Schlußfolgerungen ziehen. |
|
 |
Aus dem ersten Satz folgt, daß Körper
die unter beliebig hohem allseitigem Druck oder Zug stehen, sich niemals
plastisch verformen, denn
tmax = ½(s1 – s3)
= 0. |
|
 |
Noch verblüffender: Zusätzliche Spannungen,
die auf einen Körper einwirken, können plastische Verformungen verhindern, denn vergrößern
eines kleinen s3 kann beispielsweise tmax
verringern. |
|
 |
Aus beiden Sätzen folgt, daß es materialspezifische
kritische Größen gibt - tkrit und sBruch
- von denen die plastischen und Brucheigenschaften des Materials abhängen. |
 |
Wir haben zwar schon
aus den Bindungspotentialen abgeleitet, bei welcher ultimativen Spannung oder Dehnung eine Bindung "aufgeht",
d.h. definitiv Bruch eintritt, aber das war eine absolute obere Grenze. Wir haben keine Aussage darüber, ob Bruch schon bei kleineren Spannungen auftreten kann, und was dann
sBruch bestimmt. |
 |
Wir haben insbesondere kein Kriterium für
tkrit. Wir sind uns aber im klaren darüber, daß tkrit
so ziemlich die wichtigste Bestimmungsgröße für das nichtelastische Verformungsverhalten eines Materials
ist. Für simplen einachsigen Zugs (s2 = s3
= 0) gilt schlicht: |
|
 |
Das Material ist spröde falls
sBruch < 2tkrit. Der Sprödbruch
tritt vor plastischer Verformung auf. Da wir annehmen können, daß tkrit (und vielleicht auch sBruch) temperaturabhängig
sind, kann das bedeuten, daß ein sprödes Material mit zunehmender Temperatur duktil wird - wie z.B Si
und Ge. |
|
 |
Im Umkehrschluß gilt, daß ein Material duktil ist,
falls
sBruch > 2tkrit. |
|
 |
Elastisches Verhalten liegt jetzt immer dann vor, falls
sowohl
s < 2tkrit
und
s < sBruch. |
 |
Für kompliziertere Spannungszustände werden die Kriterien etwas komplizierter,
aber die Schlußfolgerung bleibt dieselbe: |
|
 |
Zwei Materialparameter - tkrit
und sBruch - bestimmen, ob ein gegebenes Material auf einen bestimmten Spannungszustand
elastisch, plastisch oder mit Bruch
reagiert. |
|
 |
Dabei ahnen wir schon, daß beide Parameter keine einfachen Zahlen sind,
sondern außer von der Temperatur noch vom Gefüge abhängen werden - von z.B. Korngröße, Versetzungsdichte,
Verunreinigungsgehalt, usw. |
|
 |
Und im Grunde wissen wir auch
schon, daß tkrit unmittelbar damit gekoppelt ist, wie leicht oder
schwer in einem gegebenen Material Versetzungen erzeugt und bewegt werden können. |
 |
Somit wird es jetzt Zeit, sich mit den beiden Materialparametern näher zu
beschäftigen. Soweit es das generelle Verhalten und den Bruch betrifft, wird das in den verbleibenden Unterkapitel
dieses Kapitels erfolgen; der kritischen Schubspannung
tkrit werden wir jedoch ein eigenes Kapitel
8 widmen. |
© H. Föll (MaWi 1 Skript)