|
Ein beliebiger Körper verformt sich elastisch unter dem Einfluß beliebiger
Kräfte. Wir beschreiben den Vorgang: |
|
|
|
 |
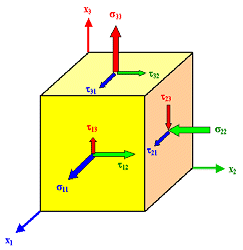
Aus einem kubischen Volumenelement dV am Punkt r
wird im allgemeinsten Fall ein "geschertes" Parallelepiped. |
|
|
 |
Analogie: Aus einem kubischen Gitter wird ein triklines. |
|
 |
Dazu muß auf jede Fläche des Kubus eine beliebige Spannung wirken können,
die wir in eine Normal- und zwei Scherspannungen zerlegen können: Þ |
|
|
 |
Die "Buchhaltung" erfolgt durch zwei Indizes: Der erste gibt die Ebene an ("i"
für die Ebene senkrecht zu xi), der zweite die Richtung ("j" für xj
Richtung). | |
|
| |
| |
 |
Anordnung der sij und tij
in Matrixform ergibt einen Tensor. Þ |
|
| sij(x,y,z) = |
æ
ç
è |
s11 t12
t13
t21 s22 t23
t31 t32 s33 |
ö
÷
ø |
| si j = s–i
–j | |
| ti j = tj i |
|
|
|
 |
Da unser dV - Würfel sich weder bewegen noch drehen soll, sind nur 6
Komponenten unabhängig. | |
| |
| |
 |
Tensoren sind Weiterführungen von Vektoren; der Spannungstensor ist ein Tensor
2. Stufe. | |
F = 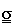 · A · A |
| Fx = sxx · Ax
+ sxy · Ay + sxz
· Az |
| Fy = syx · Ax
+ syy · Ay + syz
· Az |
| Fz = szx · Ax
+ szy · Az + szz
· Az |
|
|
|
 |
Skalare = Tensoren 0. Stufe
Vektoren = Tensoren 1. Stufe (1 Unterstrich)
Spannungen, Dehnungen = Tensoren 2. Stufe (2 Unterstriche)
(E-Modul = Tensor 4. Stufe). |
|
|
 |
Tensoren 2. Stufe verknüpfen Vektorfelder, so dass ein lokaler Vektor, z.B. ein
lokaler Oberflächennormalenvektor A durch Multiplikation mit dem Tensor in einen anderen Vektor
transformiert wird; im Beispiel in die auf die Oberfläche wirkende Kraft F. Þ |
|
|
 |
Der einfachst mögliche Fall einer solchen Verknüpfung ist, dass jede Komponenten
des Kraftvektors von jeder Komponente des Oberflächennormalenvektors abhängt: |
|
|
| |
| |
 |
Die Verknüpfung von Spannungstensor
sij und dem zugehörigen Dehnungstensor
eij braucht im allgemeinsten Fall jetzt einen Tensor 4. Stufe
mit 81 Komponenten; die cijkl
heißen elastische Koeffizienten. Þ |
|
| s11 = |
c11 11 · e11 + c11
12 · e12 + c11 13 · e13
+ c11 21 · e21 + c11 22 · e22
+ c11 23 · s23
+ c11 31 · e31 + c11 32 · e32 + c11
33 · e33 |
| s12 = |
c12 11 · e11 + ....
| | | ........... |
|
|
 |
Mit Symmetrieüberlegungen läßt sich (für die hier immer unterstellten
Einkristalle) die Zahl der elastischen Koeffizienten reduzieren: |
|
|
 |
Im "schlimmstmöglichen" Fall (trikline
Symmetrie) werden 21 elastische Koeffizienten gebraucht. |
|
|
 |
Im einfachsten Fall (kubische Gitter), reichen 2
- daraus lassen sich dann unsere altbekannte elastische Module wie E, n, G
oder K ableiten. | |
| | |
|
|
| |
|
© H. Föll (MaWi 1 Skript)