Basic elementary functions as (section 2.3):
\(e^x\), ln \(x\), \(a^x\), log\(_a x\), \(x^n\), \(\sum_{k=0}^K
a_k x^k\)
sin \(x\), cos \(x\), tan \(x\), cot \(x\),
arcsin \(x\), arccos \(x\), arctan \(x\), arccot \(x\)
”Nearly” elementary functions:
sinh \(x\), cosh
\(x\), tanh \(x\), coth \(x\), arsinh \(x\), arcosh \(x\), artanh
\(x\), arcoth \(x\)
Properties of these functions, e.g. \(e^x e^y = e^{x+y}\)
\(\sin(x+y) = \sin x \cos y + \cos x \sin y\)
Calculus of functions with one variable will be briefly recapitulated (see section 3.1), e.g.
-
\(\frac{d}{dx} \left(x^n \right) = n x^{n-1}\), \(f(x) = x^n\) \(f'(x) = n x^{n-1}\)
-
\(\int e^{-x} = - e^{-x} + C\)
-
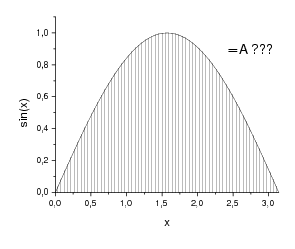
\(A = \int_0^{\pi} \sin x dx = [-\cos x]_0^{\pi} = - (-1) - (-1) = 2\) (units)
-
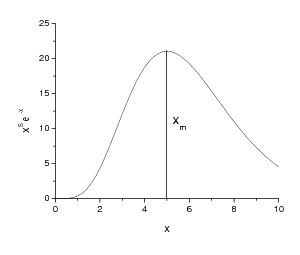
Maximum of \(f(x) = x^5 e^{-x}\) for \(x\gt0\):
\(f'(x) = 5 x^4 e^{-x} - x^5 e^{-x} = e^{-x} x^4 (5-x)\), \(f'(x_m) = 0 \Rightarrow x_m = 5\)
Vector algebra in 3D (see section 2.6)
-
Adding vectors
\(\vec a + \vec b\)
\(\vec a - \vec b = \vec a + (-\vec b)\)
\(\vec 0 \equiv\) Zero Vector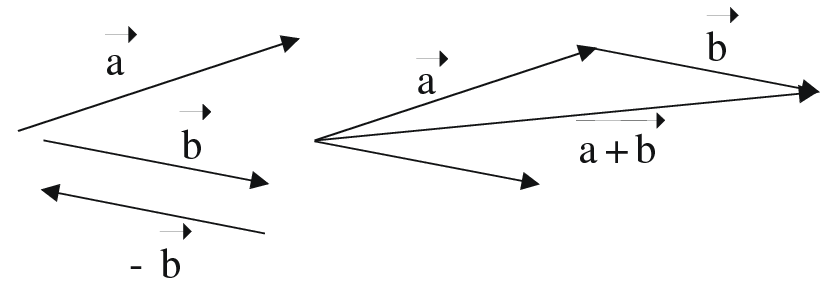
-
Scalar multiplication: \(\alpha \vec a\) stretching of \(\vec a\) by a factor of \(\alpha\) (real number)
-
Coordinates:
\(\vec a = \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right)\), \(\vec 0 = \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right)\), \(\vec b = \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right)\),
\(\vec a \pm \vec b = \left( \begin{array}{c} a_1 \pm b_1 \\ a_2 \pm b_2 \\ a_3 \pm b_3 \end{array} \right)\), \(\alpha \vec a = \left( \begin{array}{c} \alpha a_1 \\ \alpha a_2 \\ \alpha a_3 \end{array} \right)\)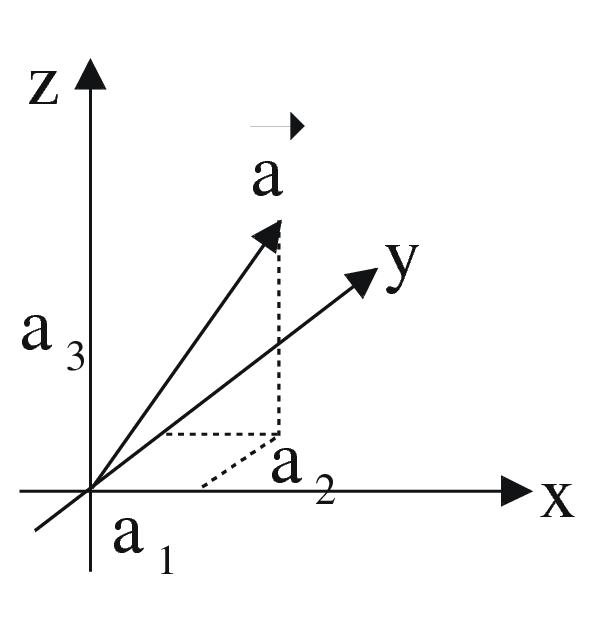
-
Modulus of vector \(\vec a\)
is its length \(|\vec a| = \sqrt{a_1^2+ a_2^2 + a_3^2}\)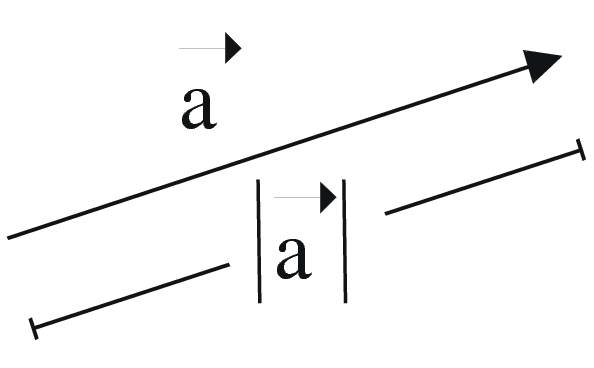
Dealing with ”Numbers” should be quite familiar, e.g. solving simple
equations:
\(x^2 - 4 x +3 = 0\),
\(\sin(\pi x) = 0\)
Complex functions as vectors of a linear vector space
-
functions: \(f(x)\) are vectors of linear vector space
-
scalar product \(\langle f|g \rangle:=\int_{-\infty}^{+\infty}f^*(x)g(x)dx\)
-
only square integrable, but complex functions (\(x\): real)
-
functions are parallel, orthonormal, angle between two functions can be calculated
-
sets of basic functions exist, projections can be calculated, ....
-
necessary for quantum mechanics
-
helpful for understanding of Fourier analysis, .....