A vector is a \(n\)-tupel of numbers:
| \[\vec{a}=\left(\begin{array}{l}x_1\\x_2\\\vdots\\x_N\end{array}\right)\; \begin{array}{c}x_1,x_2,\ldots,x_n\in\mathbb{R}\\\vec{a}\in\mathbb{R}^N\end{array}\qquad\mbox{(often $N$ = 2 or $N$ = 3)}\] |
Definition 15
| \[\begin{array}{cl}\oplus&\vec{a}+\vec{b}=\left(\begin{array}{c}a_1\\\vdots\\a_N\end{array}\right)+\left(\begin{array}{c}b_1\\\vdots\\b_N\end{array}\right)=\left(\begin{array}{c}a_1+b_1\\\vdots\\ a_N+b_N \end{array}\right)\\\\ &\mbox{zero element}\;\vec{0}=\left(\begin{array}{c}0\\\vdots\\0\end{array}\right), \qquad \mbox{inverse element}\;-\vec{a}=\left(\begin{array}{c}-a_1\\\vdots\\-a_N\end{array}\right)\\\\ &\vec{a}-\vec{b}=\vec{a}+(-\vec{b}), \qquad \vec{a}+(-\vec{a})=\vec{0}\\ \underbrace{\otimes}_{\mbox{\small scalar multiplication}} &\lambda\in\mathbb{R}\;\;\lambda\vec{a}=\left(\begin{array}{c}\lambda a_1\\\vdots\\\lambda a_N\end{array}\right)\Rightarrow\\ \end{array}\] |
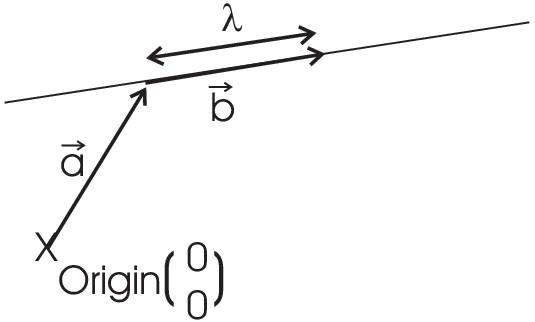
Example: These \(n\)-tupels follow the definitions 11 and 12. A line in \(N\)-D space is given by \(\vec{a}+\lambda\vec{b}\;\;\lambda\in\mathbb{R},\vec{a},\vec{b}\in\mathbb{R}^N\)

Definition 16
| \[\begin{array}{l}\left[a_1,\ldots,a_k\right],\;\lambda_1,\ldots,\lambda_k\in\mathbb{R}\\\\ \lambda_1\vec{a}_1+\lambda_2\vec{a}_2+\ldots+\lambda_k\vec{a}_k=\sum_{j=1}^k\lambda_j\vec{a}_j\quad\mbox{ is a linear combination of the vectors }\vec{a}_1,\ldots,\vec{a}_k\end{array}\] |
Definition 17 Set of vectors \(\left[\vec{a}_1,\ldots,\vec{a}_k\right]\) is called linearly independent if: \begin{eqnarray*} \lambda_1\vec{a}_1+\lambda_2\vec{a}_2+\ldots+\lambda_k\vec{a}_k&=&\sum_{j=1}^k\lambda_j\vec{a}_j=0\\ \Rightarrow\lambda_1&=&\lambda_2=\ldots=\lambda_k=0\end{eqnarray*}
Example:
| \[\vec{a}_1=\left(\begin{array}{c}1\\2\\3\\4\end{array}\right),\;\;\vec{a}_2=\left(\begin{array}{c}4\\3\\2\\1\end{array}\right),\;\;\vec{a}_3=\left(\begin{array}{c}1\\1\\1\\-1\end{array}\right)\;\;\mbox{linearly independent?}\] |
| \[\lambda_1\vec{a}_1+\lambda_2\vec{a}_2+\lambda_3\vec{a}_3=\left(\begin{array}{c}\lambda_1+4\lambda_2+\lambda_3\\2\lambda_1+3\lambda_2+\lambda_3\\3\lambda_1+2\lambda_2+\lambda_3\\4\lambda_1+1\lambda_2-\lambda_3\end{array}\right)=\vec{0}=\left(\begin{array}{c}0\\0\\0\\0\end{array}\right)\] |
only if \(\lambda_1=\lambda_2=\lambda_3=0\rightarrow\) linearly independent.
But if: \(\vec{a}_1,\vec{a}_2 \) as before and \(\vec{a}_3=\left(\begin{array}{c}6\\7\\8\\9\end{array}\right)
\) then: \(2\vec{a}_1+\vec{a}_2-\vec{a}_3=\vec{0}\)
\(\lambda_1=2,\;\lambda_2=1,\;\lambda_3=-1
\) also possible to build \(\vec{0} \Rightarrow\left[\vec{a}_1,\vec{a}_2,\vec{a}_3\right]\) linear dependent!
Definition 18 The dimension \(N\) of a vector space is the maximum number of linear independent vectors which can be found. Any such set of \(N\) linearly independent vectors is called a base of the vector space.
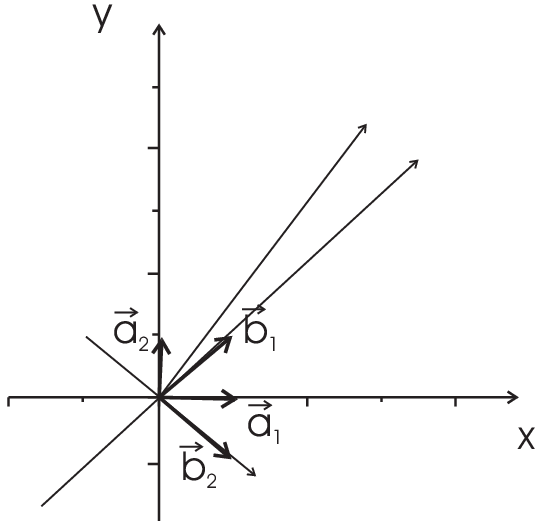
Example: \begin{eqnarray*}\vec{x}\in \mathbb{R}^N,\;\;\left[\vec{a}_1,\ldots,\vec{a}_N\right] \mbox{ base}&:&\,\vec{x}=\lambda_1\vec{a}_1+\ldots+\lambda_N\vec{a}_N\\ \lambda_1,\ldots,\lambda_N&-&\mbox{coordinates of vector $\vec{x}$ with respect to the base }\left[\vec{a}_1,\ldots,\vec{a}_N\right]\end{eqnarray*}
Example:
| 
|
\(\mathbb{R}^N\) most important vector space in the following but, \(\mathbb{C}^N\) also possible since
| \[\vec{a}=\vect{z_1\\\vdots\\z_N}\;z_1,\ldots,z_N\in\mathbb{C}\] |
is a vector, scalar multiplication is equivalent to multiplication of complex numbers and so on, but since
| \[\vect{z_1\\\vdots\\z_N}=\vect{x_1\\\vdots\\x_N}+i\vect{y_1\\\vdots\\y_N}\] |
vectors in \(\mathbb{C}^N\) are equivalent to vectors in \(\mathbb{R}^{2N}\).
Complex numbers itself are vectors in space \(\mathbb{R}^2\)
| \[z=x+iy=x\underbrace{\vect{1\\0}}_{1}+y\underbrace{\vect{0\\1}}_{i}\] |
\(\Rightarrow\) here even multiplication defined by: \(\vect{a_1\\a_2}\cdot\vect{b_1\\b_2}=\vect{a_1b_1-a_2b_2\\a_1b_2+a_2b_1}\rightarrow \mbox{complex multiplication}\)
We will now discuss the last steps of the proof to show under which condition sets of linear equations can generally be solved. Just for simplicity of writing we use the example of the dimension of a vector space \(N = 3\). So we know there exists a set of 3 vectors \(\vec{a}_i\) for which holds
| \[\lambda_1 \vec{a}_1 + \lambda_2 \vec{a}_2 +\lambda_3 \vec{a}_3 = \vec{0} \quad \Rightarrow \quad \lambda_1 = \lambda_2 = \lambda_3 = 0\] |
Taking a fourth vector \(\vec{a}_4\) and writing down the linear combination
| \[\lambda_1 \vec{a}_1 + \lambda_2 \vec{a}_2 +\lambda_3 \vec{a}_3 +\lambda_4 \vec{a}_4= \vec{0}\] |
not all \(\lambda_i\) can be zero, especially \(\lambda_4 \neq 0\) (otherwise we would have a 4 dimensional space). So we can rearrange the above equation
| \[\vec{a}_4 = -\frac{\lambda_1}{\lambda_4} \vec{a}_1 -\frac{\lambda_2}{\lambda_4} \vec{a}_2 -\frac{\lambda_3}{\lambda_4} \vec{a}_3\] |
which implies that any vector \(\vec{y}=\vec{a}_4\) can always be written as a linear combination of a set of base vectors. Defining a matrix \(\tilde{A}\) and a vector \(\vec{x}\) by
| \[\tilde{A} = \left( \vec{a}_1 \; \vec{a}_2 \; \vec{a}_3 \right) \quad \mbox{and} \quad \vec{x} = \vect{\lambda_1\\\lambda_2\\\lambda_3}\] |
we now see that any linear equation
| \[ \vec{y} = \tilde{A} \; \vec{x}\] |
has a solution if the set of (column-) vectors which form the matrix \(\tilde{A}\) is linearly independent. This is the essence of linear algebra. In what follows we will just learn several versions of more elegant and easy ways (e.g. determinants) to check for linear independence.
© J. Carstensen (Math for MS)