| 
| 
|
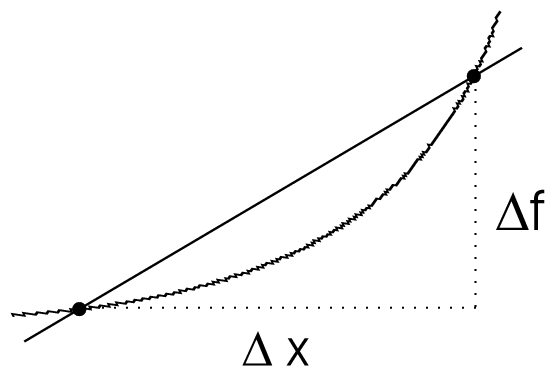
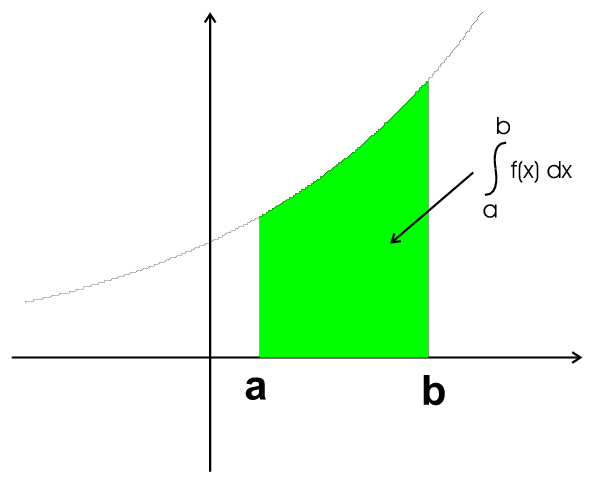
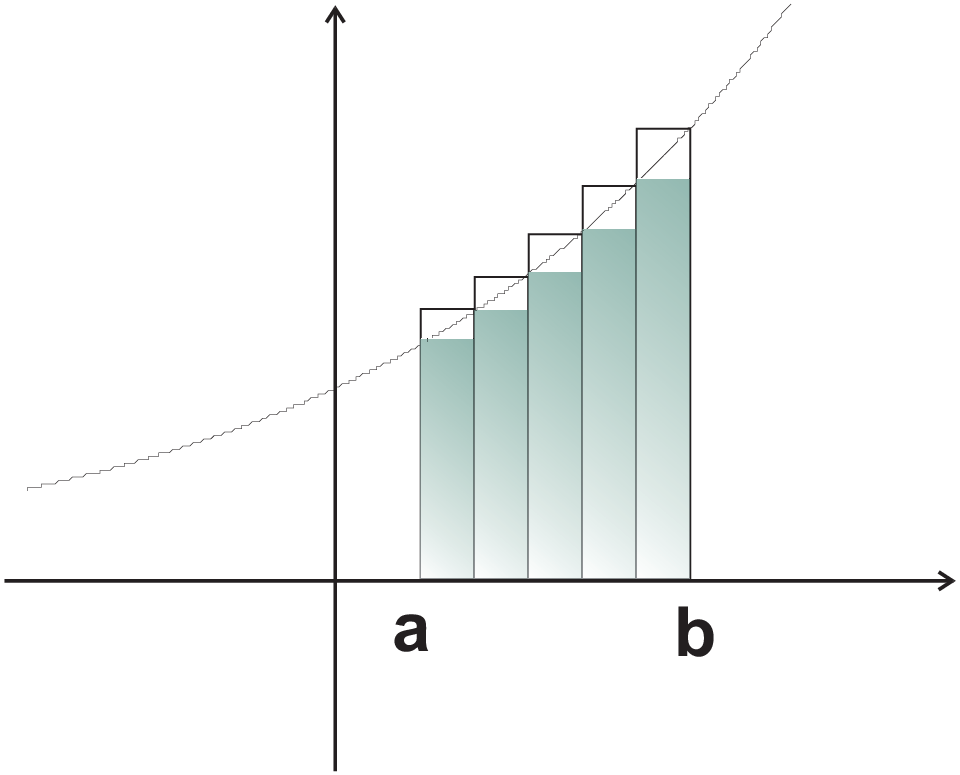
| slope of secant \(\rightarrow\) slope of tangent | integral | approximation of integral |
Function:
\(f(x), x\in \mathbb{R}, f(x)\in\mathbb{R};\) function \(f\) should behave ”normal”

| 
| 
|
| slope of secant \(\rightarrow\) slope of tangent | integral | approximation of integral |
Definition 30 Derivative of \(f\) at the point \(x\): \begin{eqnarray*}f'(x)&=&\lim_{h\to0}\frac{f(x+h)-f(x)}{h}=\lim_{\Delta x\to0}\frac{\Delta f}{\Delta x}=\overbrace{\frac{\mbox{d}f}{\mbox{d}x}}^{\mbox{Leibniz notation}}\hat{=}\mbox{$\frac{df}{dx}$-ratio of differentials}\\\\ \frac{\Delta f}{\Delta x}&=&\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{f(x)-f(x_0)}{x-x_0}\,\hat{=}\,\mbox{ratio of differences}\end{eqnarray*}
Example \begin{eqnarray*}f(x)&=&x^3;\qquad f(x+h)=(x+h)^3=x^3+3hx^2+3h^2x+h^3\\ \frac{f(x+h)-f(x)}{h}&=&3x^2+3hx+h^2\,\rightarrow\,3x^2\,\mbox{if $h\rightarrow0$}\\ \Rightarrow\,f'(x)&=&3x^2\\ \quad \Rightarrow \quad && \mbox{tedious work, rules will simplify all this considerably!!}\end{eqnarray*}
Definition 31 Integral of \(f\) between the two points \(a\) and \(b\), \(a\times b\) \begin{eqnarray*}\int\limits_a^b f(x)dx&=&\lim_{n\to\infty}\sum_{k=1}^n \Delta x\,f(a+k\Delta x)\qquad\mbox{with}\;\Delta x=\frac{b-a}{n}\\ &=&\left(\lim_{n\to\infty}\sum_{k=0}^{n-1} \Delta x\,f(a+k\Delta x)\right)\\\sum^n&\gt&\int\limits_a^b\gt\sum^{n-1}\,\rightarrow\,\mbox{''Riemann-Integral''}\end{eqnarray*}
In general: \(\Delta x\) don’t have to be the same for all \(k\).
Example: \begin{eqnarray*} f(x)&=&x^3\quad a=0,\; b=1\,\rightarrow\,\Delta x=\frac{1}{n}\\ f(a+\frac{k}{n})&=&(a+\frac{k}{n})^3=a^3+3\frac{k}{n}a^2+3\frac{k^2}{n^2}a+\frac{k^3}{n^3}\end{eqnarray*}
\begin{eqnarray*}\quad\rightarrow\quad&&\sum_{k=1}^n \Delta x\,f(x+k\Delta x)=\sum_{k=1}^n (\frac{1}{n}a^3+3\frac{k}{n^2}a^2+3\frac{k^2}{n^3}a+\frac{k^3}{n^4})\\ \quad\rightarrow\quad&&\mbox{difficult to perform further: we take: } a = 0\\ &&\left(\sum_{k=1}^n k=\frac{n(n+1)}{2},\quad\sum_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}\right)\\ &&\sum_{k=1}^n k^3=\frac{n^2(n+1)}{4}\\ \rightarrow\sum_{k=1}^n\Delta x\,f(a+k\Delta x)&=&\sum_{k=1}^n\frac{k^3}{n^4}=\frac{n^2(n+1)^2}{n^4 4}=\frac{(n+1)^2}{n^2}\frac{1}{4}\\ &\stackrel{n\to\infty}{\rightarrow}&\frac{1}{4}\Rightarrow \int\limits_0^1 x^3 dx=\frac{1}{4}\\ \quad \Rightarrow \quad&&\mbox{tedious work, integration rules will help but it is still difficult} \end{eqnarray*}
© J. Carstensen (Math for MS)