|
In contrast to dia- and paramagnetism, ferromagnetism
is of prime importance for electrical engineering. It is, however, one of the most difficult
material properties to understand. |
|
 |
It is not unlike "ferro"electricity,
in relying on strong interactions between neighbouring atoms having a permanent magnetic moment m stemming
from the spins of electrons. |
|
 |
But while the interaction between electric dipoles can, at least in principle, be understood
in classical and semi-classical ways, the interaction between spins of electrons is an exclusively
quantum mechanical effect with no classical analogon. Moreover, a theoretical treatment of the three-dimensional
case giving reliable results still eludes the theoretical physicists. |
|
 |
Originally I planned to present a very simplified theory of ferromagnetism based on spin-spin
interaction - but forget it. It's rather complex but doesn't go very far. Just accept the fact that only Fe, Co,
Ni (and some rare earth metals) show strong interactions between spins to result in (room temperature) ferromagnetism
of elemental crystals. |
|
 |
In compounds, however, many more substances exist with
spontaneous magnetization coming from the coupling of spins. |
 |
There is, however, a relatively simple theory of ferromagnetism,
that gives the proper relations, temperature dependences etc., - with one major drawback: It starts with an unphysical
assumption. |
|
 |
This is the mean field theory or
the Weiss
theory of ferromagnetism. It is a phenomenological theory based on a central
(wrong) assumption: |
|
|
Substitute the elusive spin - spin interaction between electrons
by the interaction
of the spins with a very strong magnetic field. |
|
|
 |
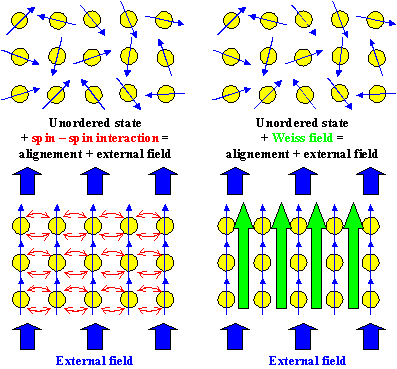
In other words, pretend, that in addition to your external
field there is a built-in magnetic field which we will call the Weiss
field. The Weiss field will tend to line up the magnetic moments - you are now treating ferromagnetism as an extreme case of paramagnetism. The scetch below illustrates this |
| |
|
 |
Of course, if the material you are looking at is
a real ferromagnet, you don't have to pretend that there is a built-in magnetic field,
because there is a large magnetic field, indeed. But this looks like mixing up cause
and effect! What you want to result from a calculation is what you start the calculation with! |
|
 |
This is called a self-consistent approach. You may view it as a closed circle, where cause
and effect loose their meaning to some extent, and where a calculation produces some results that are fed back to the beginning
and repeated until some parameter doesn't change anymore. |
|
 |
Why are we doing this, considering that this approach is rather questionable?
Well - it works! It gives the right relations, in particular the temperature dependence of the magnetization. |
 |
The local magnetic field Hloc for an external field Hext
then will be |
| |
|
|
 |
Note that this has not much to do with the local
electrical field in the Lorentz treatment. We call it "local" field, too, because it is supposed to contain
everything that acts locally, including the modifications we ought to make to account
for effects as in the case of electrical fields. But since our fictitious "Weiss field" is so much larger than
everything coming from real fields, we simply can forget about that. |
 |
Since we treat this fictive field HWeiss
as an internal field, we write it as a superposition of the external field H
and a field stemming from the internal magnetic polarization J: |
| |
|
|
 |
With J =
magnetic polarization and w =
Weiss's factor; a constant that now contains the physics of
the problem. |
 |
This is the decisive step. We now identify the Weiss field with the magnetic polarization
that is caused by it. And, yes, as stated above, we now do mix up cause and effect to some degree: the fictitiuos Weiss
field causes the alignments of the individual magnetic moments which than produce a magnetic polarization that causes the
local field that we identify with the Weiss field and so on. |
|
 |
But that, after all, is what happens: the (magnetic moments
of the) spins interact causing a field that causes the interaction, that ....and so on . If your mind boggles a bit, that
is as it should be. The magnetic polarization caused by spin-spin interactions and mediating spin-spin interaction just
is - asking for cause and effect is a futile question. |
|
 |
The Weiss factor w
now contains all the local effects lumped together - in analogy to the Lorentz treatment of local fields, µ0, and the interaction
between the spins that leads to ferromagnetism as a result of some fictive field. |
|
 |
But lets be very clear: There is no internal magnetic
field HWeiss in the material before the spins become aligned. This completely fictive field
just leads - within limits - to the same interactions you would get from a proper quantum mechanical treatment. Its big
advantage is that it makes calculations possible if you determine the parameter w experimentally. |
 |
All we have to do now is to repeat the calculations done for paramagnetism, substituting
Hloc wherever we had H. Lets see where this gets us. |
| |
 |
What we really want is the magnetic polarization J as a function
of the external field H. Unfortunately we have a transcendental equation
for J which can not be written down directly without a "J" on the right-hand side. |
|
 |
What we also like to have is the value of the spontaneous magnetization J
for no external field, i.e. for H = 0. Again, there is no analytical solution for this case. |
|
 |
There is an easy graphical solution, however: We actually have two
equations for which must hold at the same time: |
|
 |
The argument b of the Langevin function is |
| |
| b | = |
m · µ0 · (H + w · J)
kT |
|
|
|
 |
Rewritten for J, we get our first equation: |
| |
| J | = |
kT · b
w · m · µ0 | – |
H
w |
|
|
|
 |
This is simply a straight line with a slope and intercept value determined by the interesting
variables H, w, and T. |
 |
On the other hand we have the equation for J, and this is our second
independent equation
. |
|
|
| J |
= N · m · µ0 · L(b) = |
N · m · µ0 · L |
æ
è |
m · µ0 · (H + w · J)
kT | ö
ø
|
|
|
|
 |
This is simply the Langevin function which we know for any numerical value for b |
 |
All we have to do is to draw both functions
in a J - b diagram |
|
 |
We can do that by simply putting in some number for b and
calculating the results. The intersection of the two curves gives the solutions of the equation for J. |
|
 |
This looks like this |
|
|
|
|
 |
Without knowing anything about b, we can draw a definite
conclusion: |
|
 |
For H = 0 we have two solutions (or none
at all, if the straight line is too steep): One for J = 0 and one for a rather large J.
|
|
 |
It can be shown that the solution for J = 0 is unstable (it disappears for an
arbitrarily small field H) so we are left with a spontaneous large magnetic polarization
without an external magnetic field as the first big result of the mean field theory. |
 |
We can do much more with the mean field theory, however. |
|
 |
First, we note that switching on an external
magnetic field does not have a large effect. J increases somewhat, but for realistic values of
H/w the change remains small. |
|
 |
Second, we can look at the temperature
dependence of J by looking at the straight lines. For T
® 0, the intersection point moves all the way out to infinity. This means that all
dipoles are now lined up in the field and L(b) becomes 1. We obtain the saturation value Jsat |
| |
|
|
 |
Third, we look at the effect of increasing temperatures.
Raising T increases the slope of the straight line, and the two points of intersection move together. When
the slope is equal to the slope of the Langevin function (which, as we
know, is 1/3), the two points of solution merge at J = 0; if we increase the slope for the straight
line even more by increasing the temperature by an incremental amount, solutions do no longer exist and the spontaneous
magnetization disappears. |
 |
This means, there is a critical temperature
above which ferromagnetism disappears. This is, of course, the Curie temperature
TC. |
|
 |
At the Curie temperature TC, the slope of the straight line and the
slope of the Langevin function for b = 0 must be identical. In formulas we obtain: |
| |
| |
dJ
db |
= | kTC
w · m · µ0 | = |
slope of the straight line |
dJ
db |
÷
÷
|
b = 0 |
= |
N · m · µ0 · |
dL(b)
db |
= | N · m · µ0
3 | |
|
|
|
 |
We made use of our old insight
that the slope of the Langevin function for b
® 0 is 1/3. |
 |
Equating
both slopes yields for TC |
| |
| TC | = |
N · m
2 · µ02 · w
3k |
|
|
 |
This is pretty cool. We did not solve an transcendental equation nor go into deep
quantum physical calculations, but still could produce rather simple equations for prime material parameters like the Curie
temerature. |
|
 |
If we only would know w, the Weiss factor! Well, we do not
know w, but now we can turn the equation around: If we know TC, we can calculate
the Weiss factor w and thus the fictive magnetic field that we need to
keep the spins in line. |
|
 |
In Fe, for example, we have TC = 1043 K, m = 2,2
· mBohr. It follows that |
|
|
| HWeiss | = |
w · J = 1.7 · 109 A/m |
|
|
|
 |
This is a truly gigantic field strength telling us that
quantum mechanical spin interactions, if existent, are not to be laughed at. |
|
 |
If you do not have a feeling of what this number means, consider the unit of H:
A field of 1,7 · 109 A/m is produced if a current of 1,7 · 109 A flows through
a loop (= coil) with 1 m2 area. Even if you make the loop to cover only 1 cm2, you still
need 1,7 · 105 A. |
 |
We can go one step further and approximate
the Langevin function again for temperatures >TC, i.e. for b
< 1 by |
| |
|
|
 |
This yields |
|
|
| J(T > TC) |
» |
N · m2 · µ02
3kT |
· | (H + w · J) |
|
|
|
 |
From the equation for TC we can extract w and insert it, arriving at
|
| |
| J(T > TC) |
» |
N · m2 · µ02
3k(T – TC) |
· | H |
|
|
|
 |
Dividing by H gives the susceptibility c for
T > TC and the final formula |
| |
| c | = |
J
H | = |
N · m2 · µ02
3k · (T – TC) |
= | const.
T – TC |
|
|
| |
|
|
 |
This is the famous Curie law for the paramagnetic
regime at high temperatures which was a phenomenological thing so far. Now we derived it with a theory and will therefore
call it Curie - Weiss law. |
 |
In summary, the mean field approach ain't that bad! It can be used for attacking
many more problems of ferromagnetism, but you have to keep in mind that it is only a description, and not based on sound
principles. |
|
|
© H. Föll (Electronic Materials - Script)