|
"Particles", i.e. atoms or molecules in a liquid or solid are basking
in electrical fields - the external field that we apply from the outside is not necessarily all they "see" in
terms of fields. |
|
 |
First, of course, there is a tremendous electrical field inside
any atom. We have after all, positive charges and negative charges separated by a distance roughly given by the diameter
of the atom. |
|
 |
Second, we have fields between atoms, quite evident for
ionic crystals, but also possible for other cases of bonding. |
 |
However, if you look at the materials at a scale somewhat larger than the atomic
scale, all these fields must average to zero. Only then do we have a field-free interior
as we always assume in electrical
engineering ("no electrical field can penetrate a metal"). |
 |
Here, however, we are looking at the effect an external field has on atoms and molecules, and it would be preposterous
to assume that what an atom "sees" as local
electrical field is identical to what we apply from the outside. |
|
 |
Since all our equations obtained so far always concerned the local
electrical field - even if we did not point that out in detail before - we now must find a relation between the external
field and the local field, if we want to use the insights we gained for understanding the behavior of dielectrics on a macroscopic
scale. |
 |
We define the local field
Eloc to be the field felt by one particle (mostly an atom)
of the material at its position (x,y,z). |
|
 |
Since the superposition principal for fields always holds, we may express Eloc
as a superposition of the external field Eex and some field Emat introduced
by the surrounding material. We thus have |
| |
|
 |
All electrical fields can, in principle, be calculated from looking at the charge distribution
r(x, y, z) in the material, and then solving the Poisson equation (which you should know). The Poisson
equation couples the charge distribution and the potential V(x, y, z) as follows: |
| |
| D = Delta operator = |
¶2V
¶x2 | + |
¶2V
¶y2 | + |
¶2V
¶z2 |
|
|
|
 |
The electrical field then is just the (negative) gradient of the potential; E
= – ÑV. |
 |
Doing this is pretty tricky, however. We can obtain usable results in a good approximation
in a much simpler way, by using the time-honored Lorentz approach
or the Lorentz model. |
|
 |
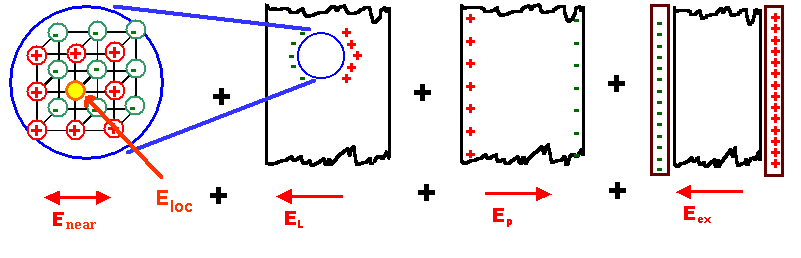
In this approach we decompose the total field into four
components. |
|
 |
For doing this, we imagine that we remove
a small sphere containing a few 10 atoms from the material. We want to know the local field in the center of this
sphere while it is still in the material; this is the local field Emat we are after. We
define that field by the force it exerts on a charge at the center of the sphere that acts as a "probe".
|
 |
The essential trick is to calculate the field produced from the atoms inside the
sphere and the field inside the now empty sphere in the material. The total local field then is simple the sum of both. |
|
 |
Like always, we do not consider the charge of the "probe" in computing
the field that it probes. The cut-out sphere thus must not contain the charge we use as the field
probe! |
|
 |
The cut-out material, in general, could produce an electrical field at its center since it
is composed of charges. This is the 1st component of the field, Enear
which takes into account the contributions of the atoms or ions inside the sphere. We will consider that field in an approximation
where we average over the volume of the small sphere. To make things clear, we look at an ionic crystal where we definitely
have charges in our sphere. |
 |
Enear, however, is not the only
field that acts on our probe. We must include the field that all the other atoms of the crystal produce in
the hollow sphere left after we cut out some material. This field now fills the "empty" void left by taking out
our sphere. |
|
 |
This field is called EL (the "L" stands
for Lorentz); it compensates for the cut-out part - and that provides our 2nd
component. |
 |
Now we only have to add the "macroscopic" fields from 1. the polarization
of the material and 2. the external field that causes everything: |
|
 |
The field Epol is induced by the macroscopic polarization
(i.e. by area charges equal to the polarization); it is the 3rd component. |
|
 |
The external field Eex = U/d from the applied voltage
at our capacitor which supplies the 4th component. |
 |
In a visualization, this looks like this: |
|
|
|
 |
The blue "sphere" cuts through the lattice (this is hard to draw). The
yellow "point" is where we consider the local field; we have to omit the contribution of the charged atom there.
We now have |
| |
| Eloc = Eex + Epol
+ EL + Enear |
|
|
 |
How large are those fields? We know the external field and also the field from the polarization
(always assuming that the material completely fills the space inside the capacitor). |
| |
|
 |
We do not know the other two fields, and it is not all that easy to find out how large they
are. The results one obtains, however, are quite simple: |
|
 |
Lorentz showed that Enear = 0 for isotropic materials,
which is easy to imagine. Thus for cubic crystals (or polycrystals, or amorphous materials), we only have to calculate EL. |
 |
EL needs some thought. It is, however, a standard problem from electrostatics
in a slightly different form. |
|
 |
In the standard problem one calculates the field in a materials with a DK given by er
that does not fill a rectangular capacitor totally, but is in the shape of an ellipsoid
including the extreme cases of a pure sphere, a thin plate
or a thin needle. The result is always |
|
|
| Eellipse = NP · |
P
er · eo |
|
|
 |
In words: The field inside a dielectric in the shape of an ellipsoid (of any shape whatsoever)
that is put between the parallel plates of a typical capacitor arrangement, is whatever it would be if the dielectric fills
the space between the plates completely times a number
NP, the value of which depends on the geometry. |
|
 |
NP is the so-called depolarization factor, a pure number, that only depends on the shape of the ellipsoid. For the extreme cases of the ellipsoid
we have fixed and well-known depolarization factors: - Thin plate: N = 1
- Needle: N = 0
- Sphere: N = 1/3
. |
 |
Our case consists of having a sphere with er = 1.
We thus obtain |
| |
|
 |
We have now all components and obtain |
|
|
| Eloc | = |
U
d | – |
P
e0 |
+ |
P
3eo |
|
|
|
 |
U/d – P/e0 is just
the field we would use in the Maxwell equations, we call it E0. It is the homogeneous
field averaged over the whole volume of the homogeneous material |
|
 |
The local field finally becomes
|
| |
|
 |
This seems a bit odd? How can the local
field be different from the average field? |
|
 |
This is one of the tougher questions one can ask. The answer, not extremely satisfying,
comes from the basic fact that all dipoles contribute to E0,
whereas for the local field you discount the effect of one
charge - the charge you use for probing the field (the field of which must not be added
to the rest!). |
|
 |
If you feel somewhat uneasy about this, you are perfectly right. What we are excluding
here is the action of a charge on itself. While we may do that because that was one
way of defining electrical fields (the other one is Maxwells equation defining a field as directly resulting from charges),
we can not so easily do away with the energy contained in the field of a single charge.
And if we look at this, the whole theory of electromagnetism blows up! If the charge is a point charge, we get infinite
energy, and if it is not a point charge, we get other major contradictions. |
|
 |
Not that it matters in everyday aspects - it is more like a philosophical aspect. If
you want to know more about this, read chapter 28 in the "Feynman
lectures, Vol. 2" |
 |
But do not get confused now! The relation
given above is perfectly valid for everyday circumstances and ordinary matter. Don't worry - be happy that a relatively
complex issue has such a simple final formula! |
© H. Föll (Electronic Materials - Script)