|
Dia- and Paramagentic propertis of materials are of no consequence whatsoever
for products of electrical engineering (or anything else!) | |
Normal diamagnetic materials: cdia
» – (10–5 - 10–7)
Superconductors (= ideal diamagnets): cSC = – 1
Paramagnetic
materials: cpara
» +10–3 |
|
|
 |
Only their common denominator of being essentially "non-magnetic" is of interest
(for a submarine, e.g., you want a non-magnetic steel) | |
|
 |
For research tools, however, these forms of magnitc behavious can be highly interesting ("paramagentic
resonance") | |
| |
| |
|
 |
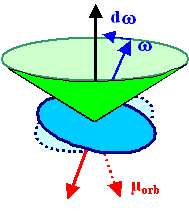
Diamagnetism can be understood in a semiclassical (Bohr) model of the atoms as
the response of the current ascribed to "circling" electrons to a changing magnetic field via classical induction
(µ dH/dt). | |
|
|
 |
The net effect is a precession of the circling electron, i.e. the normal vector of its orbit
plane circles around on the green cone. Þ |
|
|
 |
The "Lenz rule" ascertains that inductive effects oppose their source; diamagnetism
thus weakens the magnetic field, cdia < 0 must apply. |
|
|
| | |
|
 |
Running through the equations gives a result that predicts a very small effect.
Þ
A proper quantum mechanical treatment does not change this very much. |
|
| cdia = –
|
e2 · z · <r>
2
6 m*e |
· ratom |
» – (10–5 - 10–7) |
|
|
| |
| |
|
 |
The formal treatment of paramagnetic materuials is mathematically completely identical
to the case of orientation polarization | |
| W(j) = – µ0 · m
· H = – µ0 · m · H · cos j |
| | Energy of magetic dipole in magnetic field |
| N[W(j)] = c · exp –(W/kT)
= c · exp | |
m · µ0 · H · cos j
kT |
= N(j) |
| | (Boltzmann) Distribution of dipoles on energy states |
| M | = |
N · m · L(b) |
| | | | | | |
| | | b |
= | µ0 · m · H
kT | | | |
|
| Resulitn Magnetization with Langevin function L(b) and argument b |
|
|
 |
The range of realistc b values (given by largest H
technically possible) is even smaller than in the case of orientation polarization. This allows tp approximate L(b) by b/3; we obtain: |
|
| |
|
| |
|
 |
Insertig numbers we find that cpara is indeed
a number just slightly larger than 0. | |
| | |
| |
|
© H. Föll (Electronic Materials - Script)