 |
According to the mean field theory, if a material is ferromagnetic, all
magnetic moments of the atoms would be coupled and point in the same direction. We now ask a few questions: |
|
 |
1.
Which direction is that going to be for a material just sitting
there? Is there some preferred internal direction or are all directions equal? In other words: Do we have to make the fictitious
Weiss field HWeiss larger in some directions compared to other ones? Of course, we wonder if some
crystallographic directions have "special status". |
|
 | 2.
What happens if an external field is superimposed in some direction that does not
coincide with a preferred internal direction? |
|
 | 3.
What happens if it does? Or if the external field is parallel
to the internal one, but pointing in the opposite direction? |
 |
The (simple) mean field theory remains rather silent on those questions. With respect to the
first one, the internal alignment direction would be determined by the direction of the fictive field HWeiss,
but since this field does not really exist, each direction seems equally likely. |
|  |
In real materials, however, we might expect that the direction of the magnetization is not totally random,
but has some specific preferences. This is certainly what we must expect for crystals. |
|
 |
A specific direction in real ferromagnetic materials could be the result of crystal anisotropies, inhomogeneities,
or external influences - none of which are contained within the mean field theory (which essentially treats perfectly isotropic
and infinitely large materials). |
 |
Real ferromagnetic materials thus are more complicated
than suggested by the mean field theory - for a very general reason: |
 |
Even if we can lower the internal energy U
of a crystal by aligning magnetic moments, we still must keep in mind that the aim is always to minimize the free enthalpy
G = U – TS of the total system. |
|
 |
While the entropy part coming from the degree of orderliness in the
system of magnetic moments has been taken care of by the general treatment in the frame work of the orientation polarization,
we must consider the enthalpy (or energy) U of the system in more detail.
So far we only minimized U with respect to single magnetic moments in
the Weiss field. |
|
 |
This is so because the mean field approach essentially relied on the fact that by aligning
the spins relative to the (fictitious) Weiss field, we lower the energy of the individual spin or magnetic moments as treated before by some energy Walign. We have |
| |
| Ualign = Urandom – Walign
|
|
|
|
 |
But, as discussed above, real materials are mostly (poly)crystals and we must expect that the real (quantum-mechanical)
interaction between the magnetic moments of the atoms are different for different directions in the crystal. There is some
anisotropy that must be considered in the Ualign part of the free enthalpy. |
|  |
Moreover, there are other contributions to U not contained in the mean field approach. Taken
everything together makes quantitative answers to the questions above exceedingly difficult. |
 |
There are, however, a few relatively simple general rules and experimental facts that help
to understand what really happens if a ferromagnetic material is put into a magnetic field. Let's start by looking at the
crystal anisotropy. |
|
Crystal Anisotropy |
| | |
 |
Generally, we must expect that there is a preferred crystallographic direction for the spontaneous
magnetization, the so-called "easy directions". If so,
it would need some energy to change the magnetization direction into some other orientations; the "hard directions". |
|
 |
That effect, if existent, is easy to measure: Put a single crystal of the ferromagnetic material in a magnetic
field H that is oriented in a certain crystal direction, and measure the magnetization of the material in that direction:
|
|
 |
If it happens to be an easy direction, you should see a strong magnetization
that reaches a saturation value - obtained when all magnetic moments point
in the desired direction - already at low field strength H. If, on the other hand, H happens
to be in a hard direction, we would expect that the magnetization only turns into the
H direction reluctantly, i.e. only for large values of H will we find saturation. |
 |
This is indeed what is observed, classical data for the elemental ferromagnets
Fe, Ni, Co are shown below: |
| |
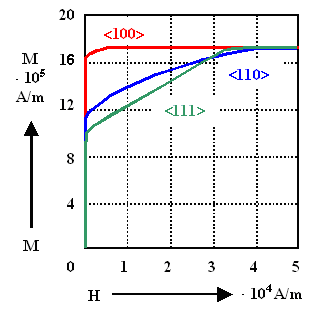
Anisotropy of magnetization in Fe. |
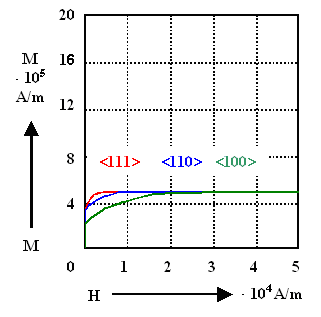
Anisotropy of magnetization in Ni. |
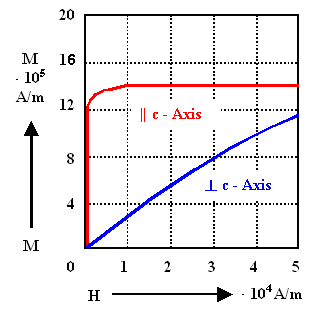
Anisotropy of magnetization in Co. |
Anisotropy of the magnetization in Fe (bcc lattice type), Ni (fcc lattice
type), and Co (hcp
lattice type). |
|
 |
The curves are easy to interpret qualitatively along the lines stated above; consider, e.g.,
the Fe case: |
|
 |
For field directions not in <100>, the spins become aligned in the <100>
directions pointing as closely as possible in the external field direction. |
|
 |
The magnetization thus is just the component of the <100> part in the field direction; it
is obtained for arbitrarily small external fields. |
|
 |
Increasing the magnetization, however, means turning spins into a "hard" directions, and this
will proceed reluctantly for large magnetic fields. |
|
 |
At sufficiently large fields, however, all spins are now aligned into the external field directions and
we have the same magnetization as in the easy direction. |
 |
The curves above contain the material for a simple little exercise: |
| |
|
| |
| Questionaire |
| Multiple Choice questions to 4.3.2 |
|
© H. Föll (Electronic Materials - Script)