4.3.3 Magnetic Domains

Reducing the External Magnetic Field

If we now turn back to the question of what you would observe for the magnetization of a single crystal of ferromagnetic material just sitting on your desk, you would now expect to find it completely magnetized in its easy direction - even in the presence of a not overly strong magnetic field.

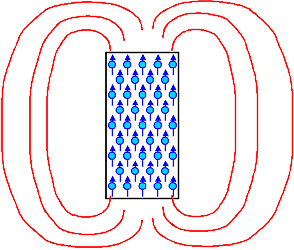
This would look somewhat like this:

There would be a large internal magnetization and a large external magnetic field H - we would have an ideal permanent magnet.

And we also would have a high energy situation, because the external magnetic field around the material contains magnetic field energy W_field.

In order to make life easy, we do not care how large this energy is, even so we could of course calculate it. We only care about the general situation: We have a rather large energy outside the material caused by the perfect line up of the magnetic dipoles in the material

How do we know that the field energy is rather large? Think about what will happen if you put a material as shown in the picture next to a piece of iron for example.

What we have is obviously a strong permanent magnet, and as we know it will violently attract a piece of iron or just any ferromagnetic material. That means that the external magnetic field is strong enough to line up all the dipoles in an other ferromagnetic material, and that, as we have seen, takes a considerable amount of energy.

The internal energy U of the system thus must be written

U_align = U_random – W_align + W_field

The question is if we can somehow lower W_field substantially - possibly by spending some smaller amount of energy elsewhere. Our only choice is to not exploit the maximum alignment energy W_align as it comes from perfect alignment in one direction.

In other words, are there non-perfect alignments patterns that only cost a little bit W_align energy, but safe a lot of W_field energy? Not to mention that we always gain a bit in entropy by not being perfect?

The answer is yes - we simply have to introduce magnetic domains.

Magnetic domains are regions in a crystal with different directions of the magnetizations (but still pointing in one of the easy directions); they must by necessity be separated by domain walls. The following figures show some possible configurations

Both domain structures decrease the external field and thus W_field because the flux lines now can close inside the material. And we kept the alignment of the magnetic moments in most of the material, it only is disturbed in the domain walls. Now which one of the two configurations shown above is the better one?

Not so easy to tell. With many domains, the magnetic flux can be confined better to the inside of the material, but the total domain wall area goes up - we loose plenty of W_align.

The energy lost by non-perfect alignment in the domains walls can be expressed as a property of the domain wall, as a domain wall energy. A magnetic domain wall, by definition a two-dimensional defect in the otherwise perfect order, thus carries an energy (per cm²) like any other two-dimensional defect.

There must be an optimum balance between the energy gained by reducing the external field, and the energy lost in the domain wall energy. And all the time we must remember that the magnetization in a domain is always in an easy direction (without strong external fields).

We are now at the end of our tether. While the ingredients for minimizing the system energy are perfectly clear, nobody can calculate exactly what kind of stew you will get for a given case.

Calculating domain wall energies from first principles is already nearly hopeless, but even with experimental values and for perfect single crystals, it is not simple to deduce the domain structure taking into account the anisotropy of the crystal and the external field energy.

And, too make things even worse (for theoreticians) there are even more energetic effects that influence the domain structure. Some are important and we will give them a quick look.

Magnetostriction and Interaction with Crystal Lattice Defects

The interaction between the magnetic moments of the atoms that produces alignment of the moments - ferromagnetism, ferrimagnetism and so on - necessarily acts as a force between the atoms, i.e. the interaction energy can be seen as a potential and the (negative) derivative of this potential is a force.

This interaction force must be added to the general binding forces between the atoms.

In general, we must expect it to be anisotropic - but not necessarily in the same way that the binding energy could be anisotropic, e.g. for covalent bonding forces.

The total effect thus usually will be that the lattice constant is slightly different in the direction of the magnetic moment. A cubic crystal may become orthorhombic upon magnetization, and the crystal changes dimension if the direction of the magnetization changes.

A crystal "just lying there" will be magnetized in several directions because of its magnetic domains and the anisotropy of the lattice constants averages out: A cubic crystal is still - on average - cubic, but with a slightly changed lattice constant.

However, if a large external field H_ex forces the internal magnetization to become oriented in field directions, the material now (usually) responds by some contraction in field direction (no more averaging out); this effect is called magnetostriction. This word is generally used for the description of the effect that the interatomic distances are different if magnetic moments are aligned.

The amount of magnetostriction is different for different magnetic materials, again there are no straight forward calculations and experimental values are used. It is a complex phenomena.

Magnetostriction is a useful property; especially since recently "giant magnetostriction" has been discovered. Technical uses seem to be just around the corner at present.

Magnetostriction also means that a piece of crystal that contains a magnetic domain would have a somewhat different dimension as compared to the same piece without magnetization.

Lets illustrate that graphically with an (oversimplified, but essentially correct) picture:

In this case the magnetostriction is perpendicular to the magnetization. The four domains given would assume the shape shown on the right hand side.

Since the crystal does not come apart, there is now some mechanical strain and stress in the system. This has two far reaching consequences

1. We have to add the mechanical energy to the energy balance that determines the domain structure, making the whole thing even more complicated.

2. We will have an interaction of domain walls with structural defects that introduce mechanical stress and strain in the crystal. If a domain wall moves across a dislocation, for example, it might relieve the stress introduced by the dislocation in one position and increase it in some other position. Depending on the signs, there is an attractive or repelling force. In any case, there is some interaction: Crystal lattice defects attract or repulse domain walls.

Generally speaking, both the domain structure and the movement of domain walls will be influenced by the internal structure of the material. A rather perfect single crystal may behave magnetically quite differently from a polycrystal full of dislocations.

This might be hateful to the fundamentalists among the physicists: There is not much hope of calculating the domain structure of a given material from first principles and even less hope for calculating what happens if you deform it mechanically or do something else that changes its internal structure.

However, we have the engineering point of view:

This is great

The complicated situation with respect to domain formation and movement means that there are many ways to influence it.

We do not have to live with a few materials and take them as they are, we have many options to tailor the material to specific needs. Granted, there is not always a systematic way for optimizing magnetic materials, and there might be much trial and error - but progress is being made.

What a real domain structure looks like is shown in the picture below. Some more can be found in the link.

We see the domains on the surface of a single crystalline piece of Ni. How domains can be made visible is a long story - it is not easy! We will not go into details here.

Summarizing what we have seen so far, we note:

1. The domain structure of a given magnetic material in equilibrium is the result of minimizing the free enthalpy mostly with respect to the energy term.

2. There are several contributions to the energy; the most important ones being magnetic stray fields, magnetic anisotropy, magnetostriction and the interaction of the internal structure with these terms.

3. The domain structure can be very complicated; it is practically impossible to calculate details. Moreover, as we will see, it is not necessarily always the equilibrium structure!

But this brings us to the next subchapter, the movement of domain walls and the hysteresis curve.

Questionaire
Multiple Choice questions to 4.3.3