|
The electric power (density) L lost per volume unit in any material
as heat is always given by |
|
|
|
|
 |
With j = current density, and E = electrical
field strength. |
 |
In our ideal dielectrics there is no direct current, only displacement currents
j(w) =dD/dt may occur for alternating voltages or electrical fields. We thus have
|
| |
| j(w) = |
dD
dt |
= e(w) ·
| dE
dt
|
= e(w) · |
d[E0 exp(iwt)]
dt |
= e(w) · i ·w · E0 · exp (iwt) = e(w) · i · w · E(w) |
|
|
|
 |
(Remember that the dielectric function
e(w) includes e0). |
 |
With the dielectric function written out as e(w) = e'(w) – i · e''(w) we obtain |
| |
| j(w) | = |
w · e'' · E(w)
| + |
i · w · e' · E(w) |
| | | |
| | | |
|
real part
of j(w);
in phase |
|
imaginary part
of j(w)
90o out of phase |
|
|
|
|
. |
 |
That part of the displacement current that is in phase
with the electrical field is given by e'', the imaginary
part of the dielectric function; that part that is 90o
out of phase is given by the real part of e(w). The power losses thus have two components |
|
|
|
|
Active power1) . |
Reactive power |
|
|
| LA |
=
|
power really lost,
turned into heat |
= w · |e''| · E2 |
|
|
| LR | = |
power extended
and recovered
each cycle |
= w · |e'| · E2 |
|
|
| |
1) Other possible expressions are:
actual power, effective power, real power, true power |
|
| |
| |
|
 |
Remember that active, or effective, or true power is energy deposited in your
system, or, in other words, it is the power that heats up your material! The reactive
power is just cycling back and forth, so it is not heating up anything or otherwise leaving direct traces of its existence. |
 |
The first important consequence is clear: |
|
 |
We can heat up even a "perfect" (= perfectly none DC-conducting
material) by an AC voltage; most effectively at frequencies around its resonance or relaxation frequency, when e'' is always maximal. |
|
 |
Since e'' for the resonance mechanisms is directly proportional to the friction coefficient kR, the
amount of power lost in these cases thus is directly given by the amount of "friction",
or power dissipation, which is as it should be. |
 |
It is conventional, for reason we will see immediately, to use the quotient of
LA /LR as a measure of the "quality" of a dielectric: this quotient
is called "tangens delta" (tg d) and we have
|
| |
LA
LR |
:= |
tg d | = |
IA
IR |
= | e''
e' |
|
|
|
 |
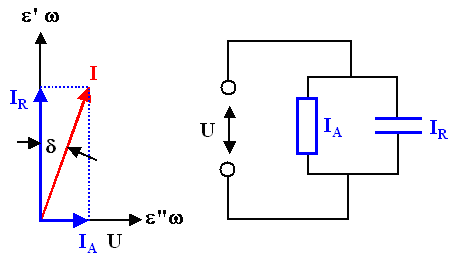
Why this somewhat peculiar name was chosen will become clear when we look at a
pointer representation of the voltages and currents and its corresponding equivalent circuit. This is a perfectly legal
thing to do: We always can represent the current from above this way; in other words we can always model the behaviour of
a real dielectric onto an equivalent circuit diagram consisting of an ideal capacitor with C(w) and an ideal
resistor with R(w). |
|
|
|
 |
The current IA flowing through the ohmic
resistor of the equivalent circuit diagram is in phase with the voltage U; it corresponds to the
imaginary part e'' of the dielectric function times w.
|
|
 |
The 90o out-of-phase current IR flowing through
the "perfect" capacitor is given by the real part e'
of the dielectric function times w. |
|
 |
The numerical values of both elements must depend on the frequency, of course - for w
= 0, R would be infinite for an ideal (non-conducting) dielectric. |
|  |
The smaller the angle d or tg d, the
better with respect to power losses. |
 |
Using such an equivalent circuit diagram (with
always "ideal" elements), we see that a real dielectric may be modeled by
a fictitious "ideal" dielectric having no losses (something that does not exist!) with an ohmic resistor in parallel
that represents the losses. The value of the ohmic resistor (and of the capacitor) must depend on the frequency; but we
can easily derive the necessary relations. |
|
 |
How large is R, the more interesting quantity, or better, the conductivity
s of the material that corresponds to R? Easy, we just have to look at the
equation for the current from above. |
|
 |
For the in-phase component we simply have |
|
|
|
|
 |
Since we always can express an in-phase current by the conductivity
s via |
| |
|
|
 |
we have |
| |
|
 |
In other words: The dielectric losses occuring in a perfect dielectric are completely contained
in the imaginary part of the dielectric function and express themselves as if the material would have a frequency dependent
conductivity sDK as given by the formula above. |
|  |
This applies to the case where our dielectric is still a perfect insulator
at DC (w = 0 Hz), or, a bit more general, at low frequencies; i.e. for sDK(w ® 0) = 0. |
 |
However, nobody is perfect! There is no perfect insulator,
at best we have good insulators. But now it is easy to see what we have to do if a real dielectric is not a perfect insulator at low frequencies,
but has some finite conductivity s0 even for w
= 0. Take water with some dissolved salt for a simple and relevant example. |
|
 |
In this case we simple add
s0 to sDK to obtain the total
conductivity responsible for power loss |
| |
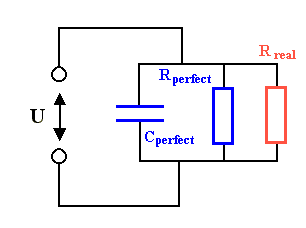 |
| stotal | = |
sperfect + sreal |
| | | |
| | = |
sDK + s0 |
|
|
|
 |
Remember: For resistors in parallel, you add the conductivities (or1/R's)
; it is with resistivities that you do the 1/Rtotal = 1/R1
+ 1/R2 procedure. |
 |
Since it is often difficult to separate sDK
and s0, it is convenient (if somewhat confusing the issue), to use stotal in the imaginary part of the dielectric function. We have |
| |
|
|
 |
We also have a completely general way now, to describe the response of any
material to an electrical field, because we now can combine dielectric behavior and conductivity in the complete dielectric
function of the material. |
|
 |
Powerful, but only important at high frequencies; as soon as the imaginary part of the "perfect"
dielectric becomes noticeable. But high frequencies is where the action is. As soon as we hit the high THz region
and beyond, we start to call what we do "Optics", or "Photonics",
but the material roots of those disciplines we have right here. |
 |
In classical electrical engineering at not too large frequencies, we are particularily interested
in the relative magnitude of both current contributions, i.e in tgd. From the pointer
diagram we see directly that we have |
| |
|
 |
We may get an expression for tg d by using for example the
Debye equations for e' and e'' derived for the dipole relaxation mechanism: |
|
|
| tg d = |
e''
e' | = |
(es – e¥) · w / w0
es + e¥
· w2/ w02 |
|
|
|
 |
or, for the normal case of e¥
= 1 (or , more correctly e0)
|
| |
| tg d = |
(es – 1) ·
w/ w0
es + w2/ w02
|
|
|
|
 |
This is, of course, only applicable to real perfect dielectrics, i.e.
for real dielectrics with s0 = 0. |
 |
The total power loss, the really interesting quantity,
then becomes (using e'' = e' · tgd,
because tgd is now seen as a material parameter)
. |
| |
|
 |
This is a useful relation for a dielectric with a given tg d
(which, for the range of frequencies encountered in "normal" electrical engineering is approximately constant).
It not only gives an idea of the electrical losses, but also a very rough estimate of the break-down strength of the material.
If the losses are large, it will heat up and this always helps to induce immediate or (much worse) eventual breakdown. |
 |
We also can see now what happens if the dielectric is not ideal
(i.e. totally insulating), but slightly conducting: |
|
 |
We simply include s0 in the definition of tgd
(and then automatically in the value of e''). |
|
 |
tg d is then non-zero even for low frequencies - there is a constant
loss of power into the dielectric. This may be of some consequence even for small tg d
values, as the example will show: |
 |
The tg d value for regular (cheap) insulation material as
it was obtainable some 20 years ago at very low frequencies (50 Hz; essentially DC) was about tg d = 0,01. |
|
 |
Using it for a high-voltage line (U = 300 kV) at moderate field strength in the dielectric
(E = 15MV/m; corresponding to a thickness of 20 mm), we have a loss of 14 kW/m3 of
dielectric, which translates into about 800 m high voltage line. So there is little wonder that high-voltage lines
were not insulated by a dielectric, but by air until rather recently! |
 |
Finally, some examples for the tg d values for commonly used
materials (and low frequencies): |
| |
| Material |
er |
tg d
x 10-4 |
Al2O3
(very good ceramic) | 10 |
5....20 | | SiO2 | 3,8 |
2 | | BaTiO3 | 500 (!!) |
150 | | Nylon | 3,1 |
10...0,7 |
Poly...carbonate,
...ethylene
...styrol | about 3 |
| PVC | 3 | 160 |
|
 |
And now you understand how the microwave oven
works and why it is essentially heating only the water contained in the food. |
|
|
|
© H. Föll (Electronic Materials - Script)