1.3.2 Ohms Law and Materials Properties

This Module comes from "Introduction to Materials Science II"; where you will find the most recent version. The link takes you there.

Required Reading

1.3.2 Ohms Law and Materials Properties

In this subchapter we will give an outline of how to progress from the simple version of Ohms "Law", which is a kind of "electrical" definition for a black box, to a formulation of the same law from a materials point of view employing (almost) first principles.

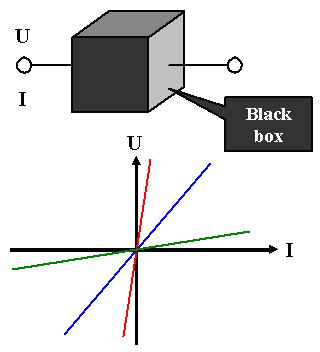
In other words: The electrical engineering point of view is: If a "black box" exhibits a linear relation between the (dc) current I flowing through it and the voltage U applied to it, it is an ohmic resistor.

That is illustrated in the picture: As long as the voltage-current characteristic you measure between two terminals of the black box is linear, the black box is called an (ohmic) resistor).

Neither the slope of the I-U-characteristics matters, nor the material content of the box.

TheMaterials Science point of view is quite different. Taken to the extreme, it is:

Tell me what kind of material is in the black box, and I tell you:

If it really is an ohmic resistor, i.e. if the current relates linearly to the voltage for reasonable voltages and both polarities.
What its (specific) resistance will be, including its temperature dependence.
And everything else of interest.

In what follows we will see, what we have to do for this approach. We will proceed in 3 steps

In the first two steps, contained in this sub-chapter we simply reformulate Ohms law in physical quantities that are related to material properties. In other words, we look at the properties of the moving charges that produce an electrical current. But we only define the necessary quantities; we do not calculate their numerical values.

In the third step - which is the content of many chapters - we will find ways to actually calculate the important quantities, in particular for semiconductors. As it turns out, this is not just difficult with classical physics, but simply impossible. We will need a good dose of quantum mechanics and statistical thermodynamics to get results.

	*1. Step: Move to specific* quantities**

	First we switch from current I and voltage U to the current density j and the field strength E, which are not only independent of the (uninteresting) size and shape of the body, but, since they are vectors, carry much more information about the system.
		This is easily seen in the schematic drawing below.

Current density j and field strength E may depend on the coordinates, because U and I depend on the coordinates, e.g. in the way schematically shown in the picture to the left. However, for a homogeneous material with constant cross section, we may write

j	=	I F

with F = cross sectional area. The direction of the vector j would be parallel to the normal vector f of the reference area considered: it also may differ locally. So in full splendor we must write

j(x,y,z) =	I(x,y,z) F	· f

The "global" field strength is

E =	U l

With l = length of the body. If we want the local field strength E(x,y,z) as a vector, we have, in principle, to solve the Poisson equation

Ñ · E(x,y,z) =	r(x,y,z) ee₀

With r(x,y,z) = charge density. For a homogeneous materisl with constant cross section, however, E is parallel to f and constant everywhere, again which is clear without calculation.

So. to make things easy, for a homogenous material of length l with constant cross-sectional area F, the field strength E and the current density j do not depend on position - they have the same numerical value everywhere.

For this case we can now write down Ohms law with the new quantities and obtain

j · F = I =	1 R	· U	=	1 R	· E · l

j	=	l F · R	· E

The fraction l/ F · R obviously (think about it!) has the same numerical value for any homogeneous cube (or homogeneous whatever) of a given material; it is, of course, the specific conductivity s

s	=	1 r	=	l F · R

and r is the specific resistivity. In words: A 1 cm³ cube of homogeneous material having the specific resistivity r has the resistance R = (r · l)/F

Of course, we will never mix up the specific resistivity r with the charge density r or general densities r, because we know from the context what is meant!

The specific resistivity obtained in this way is necessarily identical to what you would define as specific resistivity by looking at some rectangular body with cross-sectional area F and length l.

The specific conductivity has the dimension [s] = W^–1cm^–1, the dimension of the specific resistivity is [r] = Wcm. The latter is more prominent and you should at least have a feeling for representative numbers by remembering

r (metal)	»	2 µWcm

r (semicoductor)	»	1 Wcm

r (insulator)	»	1 GWcm

Restricting ourselves to isotropic and homogenoeus materials, restricts s and r to being scalars with the same numerical value everywhere, and Ohms law now can be formulated for any material with weird shapes and being quite inhomogeneous; we "simply" have

j	=	s	· E

Ohms law in this vector form is now valid at any point of a body, since we do not have to make assumptions about the shape of the body.

Take an arbitrarily shaped body with current flowing through it, cut out a little cube (with your "mathematical" knife) at the coordinates (x,y,z) without changing the flow of current, and you must find that the local current density and the local field strength obey the equation given above locally.

j(x,y,z)	=	s	· E(x,y,z)

Of course, obtaining the external current I flowing for the external voltage U now needs summing up the contributions of all the little cubes, i.e. integration over the whole volume, which may not be an easy thing to do.

Still, we have now a much more powerful version of Ohms law! But we should now harbor a certain suspicion:

There is no good reason why j must always be parallel to E. This means that for the most general case s is not a scalar quantity, but a tensor; s = s_ij.
(There is no good way to write tensors in html; we use the _ij index to indicate tensor properties.

Ohms law then writes

j_x = s_x_x · E_x + s_x_y · E_y + s_x_z · E_z j_y = s_y_x · E_x + s_y_y · E_y + s_y_z · E_z j_z = s_z_x · E_x + s_z_y · E_y + s_z_z · E_z

For anisotropic inhomogeneous materials you have to take the tensor, and its components will all depend on the coordinates - that is the most general version of Ohms law.

Note that this is not so general as to be meaningless: We still have the basic property of Ohms law: The local current density is directly proprotional to the local field strength (and not, for example, to exp– [const. · E] ).

Our goal now is to find a relation that allows to calculate s_ij for a given material (or material composite); i.e. we are looking for

s_ij = s_ij(material, temperature, pressure, defects... )

2. Step: Describe s_ij in Terms of the Carrier Properties

Electrical current needs mobile charged "things" or carriers that are mobile. Note that we do not automatically assume that the charged "things" are always electrons. Anything charged and mobile will do.

What we want to do now is to express s_ij in terms of the properties of the carriers present in the material under investigation.

To do this, we will express an electrical current as a "mechanical" stream or current of (charged) particles, and compare the result we get with Ohms law.

First, lets define an electrical current in a wire in terms of the carriers flowing through that wire. There are three crucial points to consider

1. The external electrical current as measured in an Ampèremeter is the result of the net current flow through any cross section of an (uniform) wire.

In other words, the measured current is proportional to the difference of the number of carriers of the same charge sign moving from the left to right through a given cross sectional area minus the number of carriers moving from the right to the left.

In short: the net current is the difference of two partial currents flowing in opposite directions:

Do not take this point as something simple! We will encounter cases where we have to sum up 8 partial currents to arrive at the externally flowing current, so keep this in mind!

2. In summing up the individual current contributions, make sure the signs are correct. The rule is simple:

The electrical current is (for historical reasons) defined as flowing from + to –. For a particle current this means:

In words: A technical current I flowing from + to – may be obtained by negatively charged carriers flowing in the opposite direction (from – to +), by positively charged carriers flowing in the same direction, or from both kinds of carriers flowing at the same time in the proper directions.

The particle currents of differently charged particles then must be added! Conversely, if negatively charged carriers flow in the same directions as positively charged carriers, the value of the partial current flowing in the "wrong" direction must be subtracted to obtain the external current.

3. The flow of particles through a reference surface as symbolized by one of arrows above, say the arrow in the +x -direction, must be seen as an average over the x -component of the velocity of the individual particles in the wire.

Instead of one arrow, we must consider as many arrows as there are particles and take their average. A more detailed picture of a wire at a given instant thus looks like this

More detailed view of charged particles moving ina wire

An instant later it looks entirely different in detail, but exactly the same on average!

If we want to obtain the net flow of particles through the wire (which is obviously proportional to the net current flow), we could take the average of the velocity components <v_+x> pointing in the +x direction (to the right) on the left hand side, and subtract from this the average <v_–x> of the velocity components pointing in the –x direction (to the left) on the right hand side.

We call this difference in velocities the drift velocity v_Dof the ensemble of carriers.

If there is no driving force, e.g. an electrical field, the velocity vectors are randomly distributed and <v_+x> = <v_–x>; the drift velocity and thus net current is zero as it should be.

Average properties of ensembles can be a bit tricky. Lets look at some properties by considering the analogy to a localized swarm of summer flies "circling" around like crazy, so that the ensemble looks like a small cloud of smoke. A more detailed treatment can be found in 1.3.5.

First we notice that while the individual fly moves around quite fast, its vector velocity v_i averaged over time t, <v_i>_t, must be zero as long as the swarm as an ensemble doesn't move.

In other words, the flies, on average, move just as often to the left as to the right, etc. The net current produced by all flies at any given instance or by one individual fly after sufficient time is obviously zero for any reference surface.

In real life, however, the fly swarm "cloud" often moves slowly around - it has a finite drift velocity which must be just the difference between the average movement in drift direction minus the average movement in the opposite direction.

The drift velocity thus can be identified as the proper average that gives the net current through a reference plane perpendicular to the direction of the drift velocity.

This drift velocity is usually much smaller than the average magnitude of the velocity <v> of the individual flies. Its value is the difference of two large numbers - the average velocity of the individual flies in the drift direction minus the average velocity of the individual flies in the direction opposite to the drift direction.

Since we are only interested in the drift velocity of the ensemble of flies (or in our case, carriers) we may now simplify our picture as follows:

Ensemble with only the drift velocity shown

We now equate the current density with the particle flux density by the basic law of current flow:

Current density j = Number N of particles carrying the charge q flowing through the cross sectional area F (with the normal vector f and |f| = 1) during the time interval t, or

j =	q · N F · t	· f

In scalar notation, because the direction of the current flow is clear, we have

j =	q · N F · t

The problem with this formula is N, the number of carriers flowing through the cross section F every second.

N is not a basic property of the material; we certainly would much prefer the carrier density n = N/V of carriers. The problem now is that we have to chose the volume V = F · l in such a way that it contains just the right number N of carriers.

Since the cross section F is given, this means that we have to pick the length l in such a way, that all carriers contained in that length of material will have moved across the internal interface after 1 second.

This is easy! The trick is to give l just that particular length that allows every carrier in the defined portion of the wire to reach the reference plane, i.e.

l = v_D · t

This makes sure that all carriers contained in this length, will have reached F after the time t has passed, and thus all carriers contained in the volume V = F· v_D · t will contribute to the current density. We can now write the current equation as follows:

j	=	q · N F · t	=	q · n · V F · t	=	q · n · F · l F · t	=	q · n · F · v_D · t F · t

This was shown in excessive detail because now we have the fundamental law of electrical conductivity (in obvious vector form)

j	=	q · n · v_D

This is a very general equation relating a particle current (density) via its drift velocity to an electrical current (density) via the charge q carried by the particles.

Note that it does not matter at all, why an ensemble of charged particles moves on average. You do not need an electrical field as driving force anymore. If a concentration gradient induces a particle flow via diffusion, you have an electrical current too, if the particles are charged.

Note also that electrical current flow without an electrical field as primary driving force as outlined above is not some odd special case, but at the root of most electronic devices that are more sophisticated than a simple resistor.

Of course, if you have different particles, with different density drift velocity and charge, you simply sum up the individual contributions as pointed out above.

All we have to do now is to compare our equation from above to Ohms law:

j	= q · n · v_D	:= s · E

We then obtain

s	=	q · n · v_D E	:=	constant

If Ohms law holds, s must be a constant, and this implies by necessity

v_D E	=	constant

And this is a simple, but far reaching equation saying something about the driving force of electrical currents (= electrical field strength E) and the drift velocity of the particles in the material.

What this means is that if v_D/E = const. holds for any (reasonable) field E, the material will show ohmic behavior. We have a first condition for ohmic behavior expressed in terms of material properties.

If, however, v_D/E is constant (in time) for a given field, but with a value that depends on E, we have s = s(E); the behavior will not be ohmic!

The requirement v_D/E = const. for any electrical field thus requires a drift velocity in field direction for the particle, which is directly proportional to E. This leads to a simple conclusion:

This is actually a rather strange result! A charged particle in an electrical field experiences a constant force, and Newtons first law tells us that this will induce a constant accelerations, i.e. its velocity should increase all the time! Its velocity therefore would grow to infinity - if there wouldn't be some kind of friction.

We thus conclude that there must exist some mechanism that acts like a frictional force on all accelerated particles, and that this frictional force in the case of ohmic behavior must be in a form where the average drift velocity obtained is proportional to the driving force.

Since v_D/E = constant must obtain for all (ohmic) materials under investigation, we may give it a name:

v_D E	=	µ	= Mobility =	Material constant

The mobility µ of the carriers has the unit
[µ] = (m/s)/(V/m) = m²/V · s.

The mobility µ (Deutsch: Beweglichkeit) then is a material constant; it is determined by the "friction", i.e. the processes that determine the average velocity for carriers in different materials subjected to the same force q · E.

Friction, as we (should) know, is a rather unspecified term, but always describing energy transfer from some moving body to the environment.

Thinking ahead a little bit, we might realize that µ is a basic material constant even in the absence of electrical fields. Since it is tied to the "friction" a moving carrier experiences in its environment - the material under consideration - it simply expresses how fast carriers give up surplus energy to the lattice; and it must not matter how they got the surplus energy. It is therefore no suprise if µ pops up in all kinds of relations, e.g. in the famous Einstein - Smoluchowski equation linking diffusion coefficients and mobility of particles.

We now can write down the most general form of Ohms law applying to all materials meeting the two requirements: n = const. and µ = const. everywhere. It is expressed completely in particle (= material) properties.

s	=	q · n · µ

The task is now to calculate n and µ from first priciples, i.e. from only knowing what atoms we are dealing with in what kind of structure (e.g. crystal + crystal defects)

This is a rather formidable task since s varies over a extremely wide range, cf. a short table with some relevant numbers.

In order to get acquainted with the new entity "mobility", we do a little exercise:

Exercise 1.3-1
Derive and dicuss numbers for µ

Since we like to give s as a positive number, we always take only the magnitude of the charge q carried by a particle.

However, if we keep the sign, e.g. write s = – e · n · µ_e for electrons carrying the charge q = – e; e = elementary charge, we now have an indication if the particle current and the electrical current have the same direction (s > 0) or opposite directions s < 0) as in the case of electrons.

But it is entirely a matter of taste if you like to schlepp along the signs all the time, or if you like to fill 'em in at the end.

Everything more detailed then this is no longer universal but specific for certain materials. The remaining task is to calculate n and µ for given materials (or groups of materials).

This is not too difficult for simple materials like metals, where we know that there is one (or a few) free electrons per atom in the sample - so we know n to a sufficient approximation. Only µ needs to be determined.

This is fairly easily done with classical physics; the results, however, are flawed beyond repair: They just do not match the observations and the unavoidable conclusion is that classical physics must not be applied when looking at the behavior of electrons in simple metal crystals or in any other structure - we will show this in the immediately following subchapter 2.1.3.

We obviously need to resort to quantum theory and solve the Schrödinger equation for the problem.

This, surprisingly, is also fairly easy in a simple approximation. The math is not too complicated; the really difficult part is to figure out what the (mathematical) solutions actually mean. This will occupy us for quite some time.

Questionaire
Multiple Choice Questions to 1.3.2