|
The frequency dependent current density j flowing through a dielectric
is easily obtained. Þ | |
| j(w) = |
dD
dt |
= e(w) ·
| dE
dt
|
= w · e'' ·
E(w) | + |
i · w · e' · E(w) | | |
| |
|
in phase |
|
out of phase |
|
|
|
 |
The in-phase part generates active power and thus heats up the dielectric, the out-of-phase
part just produces reactive power | |
|
 |
The power losses caused by a dielectric are thus directly proportional to the
imaginary component of the dielectric function | |
| |
| LA |
=
|
power turned
into heat |
= w · |e''| · E2 |
|
| |
|
| |
| |
 |
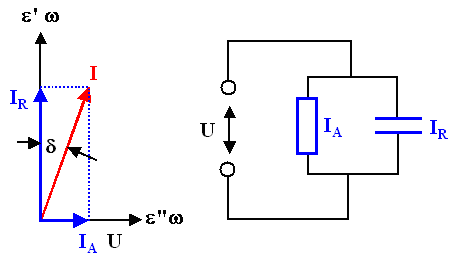
The relation between active and reactive power is called "tangens Delta"
(tg(d)); this is clear by looking at the usual pointer diagram of the current |
|
|
| |
LA
LR |
:= | tg d |
= | IA
IR |
= | e''
e' |
|
| |
|
| | |
| |
 |
The pointer diagram for an ideal dielectric s(w = 0) = 0can always be obtained form an (ideal) resistor R(w)
in parallel to an (ideal) capacitor C(w). |
|
|
 |
R(w) expresses the apparent conductivity sDK(w) of the dielectric, it follows that |
|
|
|
| |
| |
| |
| |
 |
For a real dielectric with a non-vanishing
conductivity at zero (or small) frequencies, we now just add another resistor in parallel. This allows to express all conductivity effects of a real dielectric in the imaginary part of its (usually measured)
dielectric function via | |
|
|
 |
We have no all materials covered with respect to their
dielectric behavior - in principle even metals, but then resorting to a dielectric function would be overkill. |
|
|
| | |
|
 |
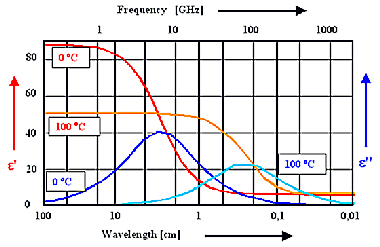
A good example for using the dielectric function is "dirty" water with
a not-too-small (ionic) conductivity, commonly encountered in food. | |
|
|
 |
The polarization mechanism is orientation polarization, we expect large imaginary parts of
the dielectric function in the GHz region. | |
|
 |
It follows that food can be heated by microwave (ovens)! |
|
| |
|
|
© H. Föll (Electronic Materials - Script)