3.3.5 Summary to: Frequency Dependence of the Dielectric Constant

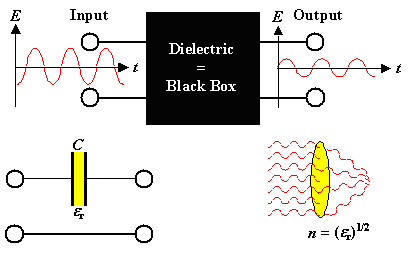
Alternating electrical fields induce alternating forces for dielectric dipoles. Since in all polarization mechanisms the dipole response to a field involves the movement of masses, inertia will prevent arbitrarily fast movements.

Above certain limiting frequencies of the electrical field, the polarization mechanisms will "die out", i.e. not respond to the fields anymore.

This might happen at rather high (= optical) frequencies, limiting the index of refraction n = (e_r)^1/2

The (only) two physical mechanisms governing the movement of charged masses experiencing alternating fields are relaxation and resonance.

Relaxation describes the decay of excited states to the ground state; it describes, e.g., what happens for orientation polarization after the field has been switched off.

From the "easy to conceive" time behavior we deduce the frequency behavior by a Fourier transformation

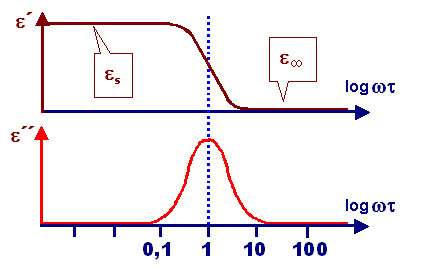
The dielectric function describing relaxation has a typical frequency dependence in its real and imaginary part Þ

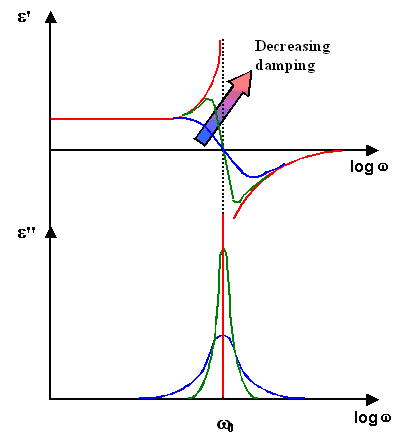
Resonance describes anything that can be modeled as a mass on a spring - i.e. electronic polarization and ionic polarization.

The decisive quantity is the (undamped) resonance frequency w ₀ = ( k_S/ m)^½ and the "friction" or damping constant k_F

The "spring" constant is directly given by the restoring forces between charges, i.e. Coulombs law, or (same thing) the bonding. In the case of bonding (ionic polarization) the spring constant is also easily expressed in terms of Young's modulus Y. The masses are electron or atom masses for electronic or ionic polarization, respectively.

The damping constant describes the time for funneling off ("dispersing") the energy contained in one oscillating mass to the whole crystal lattice. Since this will only take a few oscillations, damping is generally large.

The dielectric function describing relaxation has a typical frequency dependence in its real and imaginary part Þ
The green curve would be about right for crystals.

The complete frequency dependence of the dielectric behavior of a material, i.e. its dielectric function, contains all mechanisms "operating" in that material.

Fictive dielectric function with all mechanisms expressed

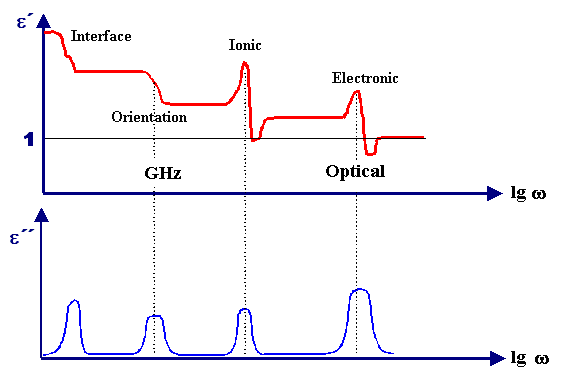
As a rule of thumb, the critical frequencies for relaxation mechanisms are in theGHz region, electronic polarization still "works" at optical (10¹⁵ Hz) frequencies (and thus is mainly responsible for the index of refraction).

Ionic polarization has resonance frequencies in between.

Interface polarization may "die out" already a low frequencies.

A widely used diagram with all mechanisms shows this, but keep in mind that there is no real material with all 4 major mechanisms strongly present!
Þ

A general mathematical theorem asserts that the real and imaginary part of the dielectric function cannot be completely independent

e'(w) =	– 2 w p		¥ ó õ 0		w^* · e''(w^) w^2– w²	· dw*

e''(w) =	2 w p		¥ ó õ 0		e'(w^) w^2– w²	· dw^*

If you know the complete frequency dependence of either the real or the imaginary part, you can calculate the complete frequency dependence of the other.

This is done via the Kramers-Kronig relations; very useful and important equations in material practice.
Þ

Questionaire
Multiple Choice questions to all of 3.3