|
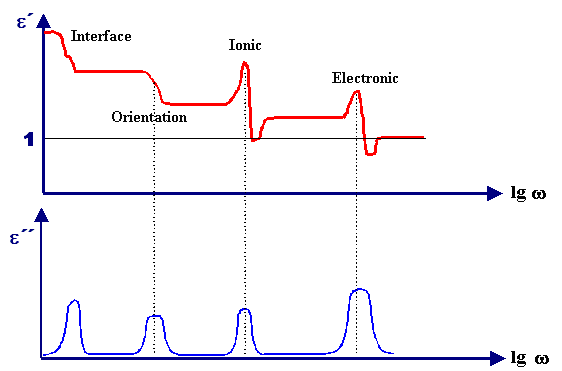
This is highly idealized - there is no material
that comes even close! Still, there is a clear structure. Especially there seems to be a correlation between the real and
imaginary part of the curve. That is indeed the case; one curve contains all
the information about the other. |
|
 |
Real dielectric functions usually are only
interesting for a small part of the spectrum. They may contain fine structures that reflect the fact that there may be more than one mechanism working at the same time, that the oscillating or relaxing particles
may have to be treated by quantum mechanical methods, that the material is a mix of several components, and so on. |
|
 |
In the link a real dielectric function
for a more complicated molecule is shown. While there is a lot of fine structure, the basic resonance function and the accompanying
peak for e'' is still clearly visible. |
 |
It is a general property of complex functions describing physical reality that
under certain very general conditions, the real and imaginary part are directly related. The relation is called Kramers-Kronig relation; it is a mathematical, not a physical property, that only demands two very general conditions to be met: |
|
 |
Since two functions with a time or frequency dependence are to be correlated, one of the requirements
is causality, the other one linearity. |
|
 |
The Kramers-Kronig relation can be most easily thought of as a transformation
from one function to another by a black box; the functions being inputs and outputs. Causality
means that there is no output before an input; linearity means that twice the input
produces twice the output. Otherwise, the transformation can be anything. |
 |
The Kramers-Kronig relation can be written as follows: For any complex function,
e.g. e(w) = e'(w)
+ ie''(w), we have the relations |
| |
|
e'(w) = |
– 2 w
p | |
¥
ó
õ
0 | |
w* · e''(w*)
w*2– w2 |
· dw* |
|
e''(w) = |
2 w
p
| |
¥
ó
õ
0 | |
e'(w*)
w*2– w2 |
· dw* |
|
|
|
 |
The Kramers-Kronig relation can be very useful for experimental work. If you want
to have the dielectric function of some materials, you only have to measure one component, the other one can be calculated. |
| |
|
|
|
|
| |
|
© H. Föll (Electronic Materials - Script)