 |
 |
| The O-lattice theory fully accounts for the structure of phase boundaries, too - as long as we look at two crystalline phases, of course. It is, however still not easy to use (it is waiting for someone to turn it into a user-friendly piece of software), and it can not answer a few specific question about the development of the structure whenever a phase boundary is formed. | |||
| So for phase boundaries, too, it is often more easy to think in terms of the simpler coincidence lattice - but with a grain of salt. A few special points are: | |||
| In general, there will be no suitable coincidence lattice at all, because the lattices are different and their lattice constants are incommensurable (their quotient is an irrational number). In practice, however, we do not know the lattice constants to an arbitrary degree of precision, and you will always find some fitting relation. | |||
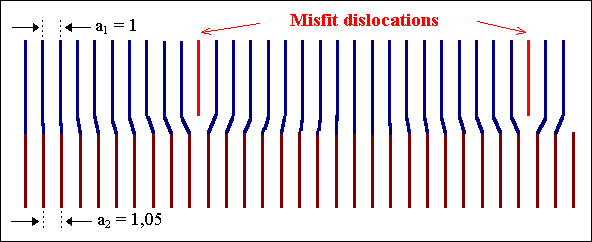
| Even if there is a CSL, it is not necessarily the proper reference lattice . This can be seen from a simple example: Two cubic crystals with lattice constants a 1 = 1 and a2 = 1,05 (i.e. a misfit of 5%) from a phase boundary: | |||
| |||
| We have a perfect two-dimensional CSL structure (S2d = 20 would hold for 2 dimensions), | |||
| Note that we can have situations (like even S numbers) which are simply not possible for grain boundaries, where the lattice constants are the same by definition. | |||
| It is much more sensible to describe this phase boundary as a S = 1 boundary with superimposed phase boundary dislocations (which we practically always will call misfit dislocations) as shown below, because this is usually an energetically better situation than a S2d = 20 (or whatever) boundary with no dislocations. | |||
| The misfit dislocations in this case are more or less lattice dislocations of the crystals - but that does not mean that DSC lattice dislocations never occur in phase boundaries! | |||
| |||
| Misfit dislocations compensate for differences in the lattice constants by concentrating the misfit in one-dimensional regions - the dislocation lines. | |||
| Between the dislocation lines the interface is coherent; a phase boundary with misfit dislocations is called semi-coherent. | |||
| Misfit dislocations - in contrast to general grain boundary dislocations - must have an edge component that accounts for the lattice constant mismatch | |||
| Whereas the O-lattice theory as applied to phase boundaries allows phase boundary dislocations in general (of which misfit dislocations are only a subset), "simple" misfit dislocations are the dominant defects in technologically important man-made phase boundaries. | |||
| Misfit dislocations are not restricted to boundaries between two chemically different types of materials. Silicon heavily doped with, e.g., Boron, has a slightly changed lattice constant and thus formally can be sen as a different phase. The rather ill defined interface between a heavily doped region and an undoped region thus may and does have misfit dislocations, an example is given in the illustration. | |||
| The mere existence of misfit dislocations coupled with their usually detrimental influence on electronic properties is the reason why many "obvious" devices do not exist at all (e.g. optoelectronic GaAs structures integrated on a Si chip), and others have problems. The aging of Laser diodes, e.g., may be coupled to the behavior of misfit dislocations in the many phase boundaries of the device. | |||
| Optoelectronics in general practically always involves having phase boundaries, e.g. devices like Lasers, LEDs, as well as all multi quantum well structures. A very careful consideration of misfit and misfit dislocations is always needed and some special process steps are often necessary to avoid these defects. | |||
| However, not every (S = 1) phase boundary with some misfit between the partners contains misfit dislocations - provided one of the phases consists of a thin layer on top of the other phase. Only if the thickness of the thin-layer phase exceeds a critical value, misfit dislocations will be observed. It is easy to understand why this is so: | |||
| For thin layers, it may be energetically more favorable to deform the layer elastically, so that a perfect match to the substrate layer is achieved. The total elastic energy contained in the "strained layer" scales with the thickness of the layer and the expenditure in elastic energy below a critical thickness for an epitaxial layer may be smaller than the energy needed to introduce misfit dislocations. | |||
| This is a situation not dealt with in the O-lattice theory or its simple CSL version. A new theory is needed. | |||
8.1.2 Energy of Misfit Dislocations and Critical Thickness | ||||||||
| The critical thickness for the introduction of misfit dislocations can be obtained by equating the energy contained in a misfit dislocation network with the elastic energy contained in a strained layer of thickness h. | ||||||||
| Since the elastic energy increases directly with h, whereas the energy contained in the dislocation network increases only very weakly with h, the thickness for which both energies are equal is the critical thickness hc. Thicker layers are energetically better off with a dislocation network, thinner layers prefer elastic distortion. | ||||||||
| This computation was first done by Frank and van der Merve in 1963; the resulting Frank and van der Merve formula became quite famous. | ||||||||
| Somewhat later in 1974 Matthews and Blakeslee reconsidered the situation and looked at the forces needed to move a few pre-existing dislocations into the interface in order to form the misfit dislocation network. They obtain the same formula for the critical thickness as van der Merve (i.e. the equilibrium situation), but their treatment also allows to consider the kinetics of the process to some extent (i.e. how the network is formed) and is therefore widely used. | ||||||||
| We are looking at the situation retrospectively by studying an article of the possibly most famous TEM and defect expert, Peter Hirsch from Oxford University, or, to be precise, Sir Peter as he must be called after his nobilitation by Elizabeth I, Queen of England. | ||||||||
| This is to show that - honorwise - a defect expert can go just as far as a rock star (several of which have been knighted by the queen - most famous the Beatles). Moneywise, however, it is a completely different matter. | ||||||||
| We use parts of his article printed in the Proceedings of the 2nd International Conference on Polycrystalline Semiconductors (Schwäbisch Hall, Germany, 1990, p. 470). Do look it up - it is part of the lecture! | ||||||||
| As you saw, great minds sometimes make great steps and are not immune to small errors! If you didn't see that, consider: | ||||||||
| How exactly do you get eq. 1? | ||||||||
| Why is the strain for minimum energy calculated in eq. 3 equal to the unrelaxed elastic strain at the point of the introduction of dislocations? | ||||||||
| What is h, the thickness of the layer, doing in an equation for the critical thickness hc (eq. 5)? After all, the critical thickness can not possibly depend on the thickness itself. | ||||||||
| Well, if you want to know, turn to the annotated version of Sir Peters paper. | ||||||||
| Still, Sir Peter got it right in principle, and his derivation of the critical thickness is short and most elegant. The final formula for the critical thickness hc is | ||||||||
| ||||||||
| With b = Burgers vector of the misfit dislocations (actually only their edge component in the plane of the interface), f = misfit parameter, i.e Da/a, e = e = 2,7183... = base of natural logarithms, and r0 = core radius of the dislocations. | ||||||||
| This transcendental equation may be roughly approximated by | ||||||||
| ||||||||
| Lets see what the calculations tell us for real phase boundaries (for a b value of 0.376 nm (which applies to Si)). We note that misfit dislocations are only to be expected if the layer thickness h exceeds the critical value hc. | ||||||||
| ||||||||
| For a misfit of 1% the critical thickness is about 4 nm - not much at all! | ||||||||
| This situation provides for many technological problems, especially in semiconductor technology. It imposes severe limits on "heterojunctions", i.e. electronic junctions between two materials because a misfit dislocation network will invariably "kill" your device - if not immediately, somewhat later (which is often worse!). | ||||||||
| Looking at common technical semiconductors, we realize that we have major problems in making heterojunctions: | ||||||||
| ||||||||
| Misfits between two materials tends to be large (not even considering Si with a lattice constant of a = 0,532 nm), and dislocation free interfaces do not come easy, if at all. | ||||||||
| A large group of researchers has been (and still is) looking for ways to beat the critical thickness limitations. There are many tricks (the link contains a few), but hard work is needed just as much as some luck and good ideas. A particularly clever recent idea known under the heading of "compliant substrates" is described in an advanced module. | ||||||||
| Experiments confirm the theory. Very thin epitaxial layers of a second phase do not show dislocations in the interface, but with increasing thickness misfit dislocations will appear. | ||||||||
| Considering that misfit dislocations are usually unwanted but that they must appear with increasing layer thickness - however not out of thin air - we ask an important question: | ||||||||
| Exactly how are misfit dislocations produced and incorporated into the interface if the critical thickness is reached. More to the point: How can I prevent this nucleation and migration process? | ||||||||
| Suffice it to say that while this question has not been fully answered, there are many ways and tricks to keep misfit dislocations from appearing at the earliest possible moment. | ||||||||
| The issue is sufficiently important in optoelectronics to merit more discussion. More information to this point can be found in various modules of the Hyperscript "Semiconductors". | ||||||||
8.1.3 Other Defects in Phase Boundaries | |||
| Even coherent phase boundaries can still contain other defects besides misfit dislocations (not to mention incoherent phase boundaries). In particular, we must expect: | |||
| Dislocation networks besides the misfit dislocations that compensate for small tilt and twist components in analogy to the small angle grain boundaries. | |||
| Steps associated with dislocations (so-called incoherent steps) in analogy to the steps encountered in grain boundaries. | |||
| Coherent steps (without any dislocation character) as something new. | |||
| After all, the surface of a substrate on which we deposit a layer of a second phase will, in general, not be atomically flat. Steps thus must be expected to be an integral part of the phase boundary. We will examine some examples for this in the next subchapter. | |||
| Next, it is important to realize that semicoherent phase boundaries can have other CSL relation besides S = 1, in particular S = 3, but other values, too. | |||
| As the most important example, consider a hexagonal lattice matched to the {111} plane of a fcc lattice . It is found to be in a S = 3 relationship, easily seen if you compare the stacking sequences in the picture below: | |||
| |||
| The ACACACA... stacking sequence of the hexagonal lattice fits right on the ABCABCA.. stacking sequence of the fcc lattice on a {111} plane. The S = 3 relationship is clearly visible; it is indicated by red dots and lines. | |||
| There are of course more complex geometries - if the CSL concept is not applicable; the O-lattice concepts has to be used. | |||
| Sorting out the various types of possible defects is no longer an easy task. The interpretation of TEM micrographs may become quite involved. | |||
| Some examples will be discussed in the case studies in the next subchapter. | |||
© H. Föll (Defects - Script)