7.3.1 The Basic Concept

7.3 O-Lattice Theory

7.3.1 The Basic Concept

Formulas here have plenty of indices, underlining etc. - and we will now give up the cursive font normally used for variables because it gets too cumbersome.

Basic Idea

The Coincidence Site lattice (CSL) provided a relatively easy way to grasp the concept of special orientations between grains that give cause for special grain boundaries. With the extension to grain boundary dislocations in the DSC lattice, the CSL concept became in principle applicable to all grain boundaries, because any arbitrary orientation is "near" a CSL orientation. But yet, the CSL concept is not powerful enough to allow the deduction of grain boundary structures in all possible cases. The reasons for this are physical, practical and mathematical:

The CSL by itself is meaningless; meaningful is the special grain boundary structure that is possible if there is a coincidence orientation. The grain boundary structure is special, because it is periodic (with the periodicity of the CSL) and contains coincidence points (cf. the picture).

But we have no guarantee that periodic grain boundary structures may not exist in cases where no CSL exists; i.e. by only looking at CSL orientation, we may miss other special orientations. That will be certainly true whenever we consider boundaries between different lattices - be it that lattice constants of the same materials changed ever so slightly because one grain has a somewhat different impurity concentration, or that we look at phase boundaries between different crystals. If the lattice constants are incommensurable, there will be no CSL at all.

As we have seen, even a CSL with S = 41 is significant, even so it is virtually unrecognizable as anything special in a drawing. This is an expression of the mathematical condition, that you either have perfect coincidence or none. If two points coincide almost, but not quite, no recognizable CSL will be seen. If two lattice points coincide except for, lets say, 0,01 nm, we certainly would say we have a physical coincidence, but mathematically we have none.

The same is true if we rotate a lattice away from a coincidence position by arbitrarily small angles. Mathematically, the coincidence is totally destroyed and the situation has completely changed, whereas physically an arbitrarily small change of the orientation would be expected to cause only small changes in properties.

Only a very small fraction of grain orientations have a CSL. The "trick" we used to transform any orientation into a coincidence orientation by introducing grain boundary dislocations in the DSC lattice is somewhat questionable: the effect (= CSL) comes before the cause (= dislocations in the DSC lattice), because at the orientation that we want to change no CSL and therefore no DSC lattice exists.

It becomes clear that the main problem lies in the discreteness of the CSL. Any useful theory for special grain boundary (and phase boundary) structures must be a continuum theory, i.e. give results for continuous variations of the crystal orientation (and lattice type).

This theory exists, it is the so-called "O-lattice theory" of W. Bollmann; comprehensively published in his opus magnus "Crystal Defects and Crystalline Interfaces" in 1970.

The O-lattice theory is not particularly easy to grasp. (Sorry, but it took me many hours, too). It is well beyond the scope of this hyperscript to go into details. What will be given is the basic concept, the big ideas; together with some formulas and a few examples. You should first read just over it, trying to get the basic ideas, than study it point by point. If you don't get it the first time - don't despair, you are in good if not excellent company!

There are two basic ideas behind the O-lattice theory:

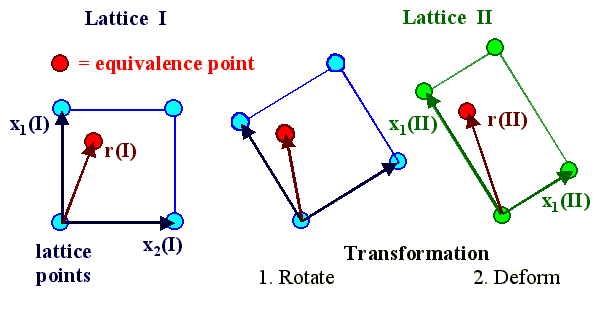
1. Take a crystal lattice I and transform it in any way you like. That means you can not only rotate it into an arbitrary orientation relative to crystal I, but also deform it by stretching, squeezing and shearing it. The crystal lattice II generated in this way from a simple cubic lattice I thus could even be an arbitrarily oriented triclinic lattice.

2. Now look for coincidence points between lattice I and lattice II. But do not restrict the search for coinciding lattice points, but expand the concept of coincidence to all "equivalence points" within two overlapping unit cells. What equivalence points are becomes clear in the illustration.

Points in lattice I and lattice II are called equivalent, if their space vectors are identical (always in their respective lattice coordinate system).

The Basic Formula

Let's look at the example illustrated above. Lattice I is deformed by first rotating it and then stretching the axis x₁; this produces lattice II

An arbitrary point within the elementary cell of lattice I is described by a vector r(I)

r(I) transforms into a vector r(II) by the transformation applied. The point reached within the unit cell of lattice II by r(II) is then an equivalence point to the one in crystal I.

Of course there is more than one equivalence point; there is always an infinite set defined by one point plus all points reachable by a lattice translation vector T from this particular point.

Any point r'(II) in lattice II belonging to the set as defined above can be described in the coordinate system of lattice II (defined by the units vectors x₁(II) and x₂(II)) by

r'(II)	=	r(II) + T(II)

With T(II) = any translation vector of lattice II, or

T(II)	=	n · x₁(II) + m · x₂(II)

And n, m = 0, ± 1, ± 2, ...

All these points are by definition equivalence points to the corresponding set of points in lattice I given by

r'(I)	=	r(I) + T(I)

Let us designate the set of all equivalence points defined above in lattice I by C₁ and the corresponding set in lattice II by C₂ and, for the sake of clarity, all vectors pointing to equivalence points of the respective sets by r(C₁) and r(C₂).

If we now look at a certain equivalence point in lattice II, it always originated from lattice I by the general transformation as shown in the picture below

The blue lattice was obtained from the pink one by some transformation; in this case by a simple rotation.

The dark point with the red vector pointing to it is an arbitrary point in lattice I (for the sake of easy recognition about in the center of a lattice I cell).

After the transformation, it is now the red point at the apex of the blue and pink arrows in lattice II. It is still about in the center of a cell in lattice II, but for the particular transformation shown, it is now also about in the center of a lattice I cell - there is (about) a coincidence of equivalence points.

Let's assume perfect coincidence, then the red point denotes coinciding equivalence points, i.e. equivalence points that are "on top of each other".

We need a precise mathematical formulation that gives us the conditions under which coincidence of equivalence points occcurs.

This is easy, we just have to consider that for coinciding equivalence points the blue vector in lattice II can be obtained in two ways:

By the transformation equation from the corresponding red vector of lattice I (valid for all equivalence points) or, since the coincidence point belongs to both lattices at once, by
adding some translation vector of lattice I to the red vector. This is symbolically shown in the picture.

In formulas we can write for any vector in lattice II pointing to some equivalent point of the set C₂:

r(C₂)	=	A {r(C₁)}

r(C₁)	=	A^–1 {r(C₂)}

With A = transformation matrix (we will encounter examples for A later; see also the basic module for matrix calculus) since this simply describes how lattice II originates from lattice I. This was the first way mentioned above.

On the other hand, we can obtain new equivalence points in lattice I, i.e. other elements of the set C₁ designated by e(C₁) quite generally by the equation

e(C₁)	=	r(C₁) + T(I)

We will now use these relations for coinciding equivalence points:

We are looking for coincidences of any one member of the set r(C₁) with any one member of the set r(C₂); any coincidence point thus obtained will be named r₀. Since this point, describable in lattice II by r(C₂) must be reachable in lattice I by first going down r(C₁) and then adding a translation vector of lattice I, we obtain

r(C₂) = r(C₁) + T(I) = r₀

Using the transformation equation for lattice I from above and substituting it into the above equation yields

r₀	=	A^–1 {r₀} + T(I)

We wrote r₀ instead of r(C₂) because we do not need the distinction between the sets C₁ and C₂ any more because r₀ belongs to both sets.

Rearranging the terms following matrix calculus by using the identity or unit transformation matrix I, we obtain the fundamental equation of O-lattice theory:

( I – A^–1 ) r₀	=	T(I)

What does that equation mean?

For a given transformation, i.e. for given orientation relationship between two grains, its solution for r₀ defines all the coincidence points or O-points of the lattices. The coincidence of lattice points is a subset of the general solution for the coincidence of equivalence points.

The question comes up if there are any solution of this equation. Algebra tells us that this requires that the determinant of the matrix, |I – A^–1|, must be ¹ 0. This will be generally true (but not always), so generally we must expect that solutions exist, i.e. that a CSL (= O-lattice) for some equivalence points (= O-points) exists - for any possible combination of lattice I and lattice II.

How do we solve the O-lattice equation, i.e. obtain the set of O-points for a given lattice and transformation? Simply by inverting the matrix we obtain:

r₀ = ( I – A^–1 )^–1 · T(I)

That is all there is to do; it looks easy. If we have a given transformation matrix A, the equation above gives us the set of vectors defining the equivalent points, or as we are going to call them, the O-points of the two lattices.

However, the diffusion equations look easy, too, but are not easy to solve. Also, we do not yet know what the solution, the O-lattice, really means with respect to grain- or phase-boundaries.

We will look at this more closely in the next paragraph; but first we will discuss a simple example.

Example for Caculating the O-Lattice

To keep the matter simple, we look at a two-dimensional situation where a square lattice rotates on top of another one. This will include our former example of the S = 5 CSL case. (A word of warning: In Bollmanns book are occasional mistakes when it comes to the S5 orientation (which is frequently used for illustrations)).

The transformation matrix is a pure rotation matrix, for the rotation angle a it writes

æ
è

cos a	– sin a
sin a	cos a

ö
ø

From this we get

A^–1

æ
è

cos a	sin a
– sin a	cos a

ö
ø

1 – A^–1

æ
è

1 – cos a	– sin a
sin a	1 – cos a

ö
ø

(1 – A^–1 )^–1

æ
è

½		– ½ cotan a/2
½ cotan a/2		½

ö
ø

Now let's do an example. The base vectors of the square lattice I are x₁(I) = (1, 0), x₂(I) = (0, 1).

If we use them as the smallest possible translation vector T(I) of lattice I, we obtain by multiplication with the last matrix the smallest vectors of the O-lattice which then must be the unit vectors of the O-lattice, u₁ and u₂:

u₁	=	æ ç è	½ ½ · cotan (a/2)	ö ÷ ø


u₂	=	æ ç è	– ½ · cotan (a/2) ½	ö ÷ ø

This is easily graphically represented, but the pictures get to be a bit complicated:

Lattice I is the blue lattice, lattice II the red one; it has been rotated by the angle a.

The unit vectors of the O-lattice can be determined by the intersection of the light- and dark-green lines (remember the definition of tan and cotan!); they are depicted in black.

The O-lattice then can be constructed, its lattice points are shown as orange blobs.

Note that a three dimensional expansion would not produce much that is new. On any plane above or below the drawing plane, the situation is exactly what we have drawn. This has one interesting consequence, however:

In three dimension, we have no longer O-points, but O-lines in this case.

The O-lattice in this case thus is not a point lattice, but a lattice of lines perpendicular to the plane of rotation. This will come up naturally later, but it is good to keep it in mind for what follows. However, since this is not the most general case, we will keep talking of O-points.

The picture neatly helps to overcome a possible misunderstanding: For any O-point, a vector from the origin of either crystal to the O-point (our vectors r(I) and r(II)) point to a coinciding equivalence point or O-point, but different points of the O-lattice may be different equivalence points. In the example we have O-points that are almost at the center of both unit cells, or almost at a lattice point of both unit cells - the O-lattice seems to be constructed of two kinds of coinciding equivalence points; but:

If we would include more cells of the O-lattice, we would see that equivalence points shift slightly for the example given. A few O-lattice cells away, they would be more off-center or more distant to a lattice point than close to the origin of the O-lattice.

Just how many equivalence points of the set of equivalence points (which has an infinite number of members) are needed for an O-lattice is an important (nontrivial) question which we will take up later again.

We can rephrase this important question:

Is the pattern of equivalence points periodic (= finite number of equivalence point) or non-periodic (infinite number)? In other words: If any one point of the O-lattice defines a specific equivalence point in the crystal lattices, does this specific point appear again at some other point in the O-lattice (apart from the trivial symmetries of the O-lattice)?

We will come back to this question later; it is the decisive feature of the O-lattice for defining the DSC-lattice.

How do we get the CSL from the O-lattice? That is easy: It must be that particular subset of all possible O-lattices where all O-points are also lattice points in both lattices.

Looking at the unit vectors of the O-lattice, however, there is no way of expressing them in integer values of the base vectors of lattice I, because one component is always 1/2. How about that?

This is not a real problem, best illustrated with an example: If we chose a = 36^o52,2', we have

u₁	=	æ ç è	½ ½ · cotan (a/2)	ö ÷ ø	=	æ ç è	1/2 3/2	ö ÷ ø


u₁	=	æ ç è	– ½ · cotan (a/2) ½	ö ÷ ø	=	æ ç è	– 3/2 1/2	ö ÷ ø

Thus every second point of the O-lattice is a lattice point in both lattices (depicting O- points of the equivalence class [0,0]), these points thus define the S = 5 CSL. The other O-points are of the equivalence class [1/2,1/2]. CSL lattices (two-dimensional case) thus correspond to specific O-lattices, but with lattice constant possibly larger by some integer value. This is quite important so we will illustrate this in a special module.

Note, too, that in this case the pattern of equivalence point is obviously periodic, so we have a first specific answer to the question asked above.

Before we delve deeper into the intricacies of O-lattice theory, we shall first discuss some of its general implications in the next paragraphs.