7.2.3 Case Studies: Small Angle Grain Boundaries in Silicon II

The recipe for "making" small angle grain boundaries in Silicon given in the preceding paragraph can be used for twist boundaries on any plane, besides the {100} plane the {111} planes are particular interesting.

The structure will be much more complicated and serves to illustrate the importance of the grain boundary plane for given orientations. The picture below is a bright-field TEM micrograph (obtained under the specific bright-field conditions that rival weak-beam resolution mentioned before) and shows all dislocations present.

This is also an example of what may happen to you when you sit down at an electron microscope with your specimen and start to look at it.

You know what to expect (a small angle twist grain boundary) in general, but now you see fascinating things - can you understand what you see?

And, in extrapolation, can you understand what you see if you do not know beforehand what to expect?

Well, we can understand most of the structure seen above. Lets construct it step by step

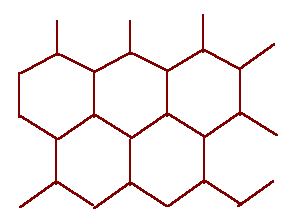
There must be a network of screw dislocations with b = a/2<110>. Since three Burgers vectors of this kind are contained in a given {111} plane, we expect a hexagonal network as shown on the left.

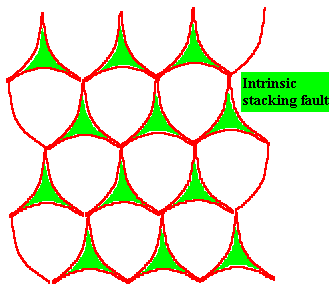
The knots where six dislocations meet can not be expected to be stable; we would expect a splitting leading to the honeycomb pattern illustrated on the left (with a changed scale for clarity).

In contrast to the {100} twist boundary, the dislocations now can split into partial dislocations in the plane of the boundary, we expect that the dislocations are split in this case. Working through the geometry we see that everything fits at one knot, it can easily be extended in the way shown. This optimizes the energy gain by large separations between the partials while at the same time keeping the stacking fault area small.

The "constricted" knots now look "funny" - again 6 dislocations meet at one point. Can we split the knot to something more favorable?

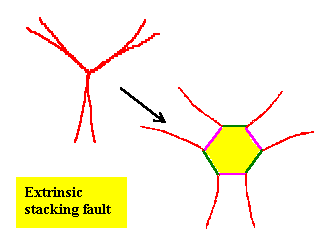
Indeed, we can, as shown on the left. However, we only can do this by introducing more Shockley dislocations and extrinsic stacking faults

Putting everything together we obtain a network of Shockley dislocations that corresponds exactly to what we see in the regular parts of the micrograph above. The exact geometry, of course, depends mainly on the stacking fault energies - here we may find differences if we would look at similar grain boundaries in other fcc materials.

It remains to explain the various non-regularities of the picture.

Most conspicuous are the large "blobs" with just a trace of some hexagonal structure. They are simply SiO₂ precipitates left over from the welding process; the hexagonal structures are Moirée patterns that always appear whenever two regular structures are put on top of each other.

The other irregularities are formed by a superposition of:

A few edge dislocations to accommodate some tilt component.

Dislocations that moved from somewhere in the crystal into the grain boundary where they were caught and incorporated into the network. These dislocations are called extraneous or extrinsic grain boundary dislocations because they are not an integral part of the grain boundary structure.

Dislocations needed to accommodate steps, i.e. changes of the grain boundary plane measuring a few atomic distances.

It is not always clear or easily analyzed exactly what it is that you see. Especially the connection between steps and intrinsic or extrinsic dislocation is, in general, quite complicated, because on the one side most, but not all grain boundary dislocations automatically introduce steps, while on the other side most, but not all steps introduce dislocations. We will deal with that matter in more detail when dealing with phase boundaries.

But we are not yet done with the low-angle twist boundary on {111}. The micrograph above shows only part of the structure. The micrograph below shows more:

The lower inset shows a magnified view of the network from the lower half of the boundary; the upper inset from the upper half. (Click on the picture for an enlargement and more information),

Whereas the lower part shows the network discussed above, the upper part shows something new: A rather simple network with reduced spacing. Detailed analysis reveals that the dislocations in the upper part have Burgers vectors b = a/6<112>, but they are not proper Shockley partials, because there are no stacking faults between the dislocations.

They are rather dislocations in the DSC lattice of a S = 3 boundary - in other words, the low angle twist boundary has split into two twin boundaries with a superimposed dislocation network in one of the twin boundaries.

We may ask: Why? And in which twin boundary are the dislocations? Why are they not in the perfect lattice between the boundaries?

It seems to ever end. But in order not to have too much detail in the main backbone part, these complications will be discussed in an advanced section.