|
|
|
Note: For ease of writing /reading in this module, variables
are not in italics; instead vectors are underlined |
| |
 |
Franks formula relates B, the sum of all the specific
Burgers vectors bi cut by a vector r lying in the plane of the boundary, to the angle
a with which one of the crystals is rotated with respect to the other one around the polar
unit vector l. It is valid for small angles (say a < 10o)
and given by
|
| |
|
|
 |
Note that we do not need three angles of rotation
as required for a general grain boundary because we do not rotate around the axis of a coordinate system, but around the
polar vector l. |
|
 |
Note also that the grain boundary plane (and thus r) is not
required to be perpendicular to l. r thus can have any direction
and length relative to l. |
 |
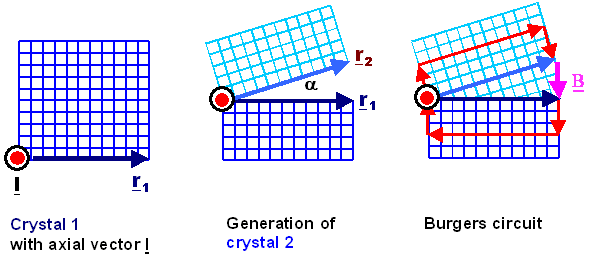
For the derivation of Franks formula we consider a small angle grain boundary
formed by rotating crystal 1 around an arbitrary axis l by a and
thus forming crystal 2. After that we join crystal 1 and crystal 2 on any plane.
|
|
 |
A vector r1 in the plane of the grain boundary (to be) in crystal 1 thus
gets transformed to a vector r2 in crystal 2. Note that r1 does
not have to be perpendicular to l. |
|
 |
Next, we make a Burgers circuit in the system with the small angle grain boundary and
a reference circuit in the perfect crystal 1 (or crystal 2). We will move along a vector r1
that is much longer than a lattice constant or the spacing of the dislocations that will make up the boundary. |
|
 |
In the perfect lattice we will start from the endpoint of r1 and move to the start
of r1 in an e.g. counter-clockwise direction. In the crystal with the grain boundary, we do the
same circuit, except that as soon as we switch over to grain 2, we follow r2. |
|
 |
The whole procedure can be illustrated as follows: |
| |
|
|
 |
There will be a closing failure B which must be identical to the sum of the Burgers vectors
of all the dislocations contained in the circuit. Only the components of the b's
lying in the plane perpendicular to l are counted, of course. |
|
 |
For clarity, the vectors r are at right angles to l in the drawing, but this
is not generally necessary. |
 |
From vector calculus
we know that a rotation can be described by an axial vector given by R = l · a.
|
|
 |
The difference vector B between the two vectors r1 and r2
(with r2 produced from r1 by the rotation) than can be written as
|
| |
|
|
 |
- and this is Franks formula from above. |
 |
Note that there are two approximations in this. First, we assume small
angles so that sin(a) »
a; and secondly, in the same vein, we assume r1»
r2 = r.
|
|
 |
Of course, we also assume that there is a smooth cross-over at the boundary (or that r is
so large that to give or take parts of a lattice constant doesn't matter). |
 |
This is a simple formula, but like most vector formulas, it has some hidden power.
Before we look into the power of Franks formula a little more closely, we will consider what it cannot
do: |
|
 |
The formula gives the net content of Burgers vectors
in a small angle grain boundary, but not necessarily the arrangements of the dislocations.
It does not, of course, say anything about possible splitting into partial dislocations either. This means that there might
be several arrangements of dislocations with the same B. The one that will be observed will be (most likely)
the one with lowest total energy. |
|
 |
No elastic distortion is considered. Between the dislocation the lattice is perfect; elastic distortion
is present only in the core regions of the dislocations. |
 |
Bearing this in mind, lets look at some special cases. Since Burgers vectors are
translation vectors of the lattice, in general three sets of non-coplanar dislocation
will be required to produce the vector B. Special cases therefore are
boundaries where only one or two sets of dislocations are needed. |
 |
If we have a boundary where one set of dislocations
with Burgers vector b1 is sufficient, B can be written as |
| |
|
|
 |
With N = number of dislocations cut by r |
 |
This obviously, looking at Franks formula, requires b to be perpendicular
to r and l. |
|
 |
The direction of r in the plane of the boundary is arbitrary; this means that b
must be at right angles to the plane of the boundary or parallel to the normal n of the boundary plane and
l must be at right angles to n; it follows that l must be contained in the boundary. |
|
 |
If we now chose the particularly simple case of r = rp being parallel to
l, we obtain (rp × l) = 0, which means that no dislocations are intersected
by rp, implying that the dislocation lines must be parallel to the rotation axis l.
|
 |
This leaves room only for the conclusion that a boundary
with only one set of dislocations must be a pure tilt boundary. |
|
 |
The spacing of the dislocations is obtained if we take r = rra at right
angles to l thus intersecting the dislocations lines at right angles, too. In this case we can write rra
as rra = r · (l × n) and obtain |
| |
| N · b | = |
a · (r × l) |
| | | |
| | = |
a ·r · [(l × n) × l] |
| | |
| | |
= |
a · r · n |
|
|
|
 |
With b = b · n and the spacing d between the dislocations given by d
= r/N, we obtain for the spacing dtilt of dislocations in a pure tilt boundary with the boundary plane
at right angles to the Burgers vector the relation used before: |
| |
|
 |
Similar considerations, which are straight forward but quite involved, can be
made for the case of small angle grain boundaries with two sets of dislocations and
the possible subsets (e.g. Burgers vectors in the plane of the boundary for pure twist boundaries). |
|
 |
For this and more, Hull and Bacons book can be consulted,
which treats these cases in detail. |
 |
More important in the development of boundary structure theories is Bollmanns interpretation of Franks formula; which is the starting point of the O-lattice
theory as will be discussed in the link. |
|
|
© H. Föll (Defects - Script)
![]() 7.2.1 Small Angle Grain Boundaries and Beyond
7.2.1 Small Angle Grain Boundaries and Beyond ![]() 7.2.2 Case Studies: Small Angle Grain Boundaries in Silicon I
7.2.2 Case Studies: Small Angle Grain Boundaries in Silicon I ![]() 7.3.3 The Significance of the O-Lattice
7.3.3 The Significance of the O-Lattice ![]() Bollmanns Interpretation of Franks Formula
Bollmanns Interpretation of Franks Formula