7.3.3 The Significance of the O-Lattice

Lets pretend we are considering an actual grain boundary. We have found a suitable transformation matrix that produces crystal II out of crystal I with the right orientation, we have solved the basic equation, and we have constructed a suitable O-lattice. What does that give us?

We now must address the essential question: What is the significance of the O-lattice for grain- and phase boundaries? What is the physical meaning? There is an easy answer and a difficult implementation:

First of all, the O-lattice in itself has no physical meaning whatsoever - in this it is exactly like the CSL.

However, since it always exists (unlike the CSL) and is defined in both crystals, if you were to design a boundary between two crystals of given orientation (and thus with one well-defined O-lattice) that intersects as many O-lattice points as possible, you will obtain the best physical fit along the boundary, i.e. probably the lowest grain boundary energies.

"Best physical fit" is not a very quantitative way of putting it. It means that the atoms to the left and right of the boundary will not have to be moved very much to the positions they will eventually occupy in the real boundary. This also can be expressed as "minimal strain" situation; the expression Bollmann uses.

If atoms happen to sit on an O-lattice point, they do not have to move at all because then then occupy equivalent positions in both crystals; if they are close to an O-lattice point, they only move very little, because at the O-points the fit is perfect.

The misfit increases moving away from an O-lattice point and reaches a maximum between O-lattice points.

The crystals then can be expected to increase the area of best fit between O-lattice points and to concentrate the misfit in the regions between O-lattice points - this will be a dislocation with Burgers vector = lattice vector. We cannot, at this stage produce grain boundary dislocations, i.e. we are still limited to small angle grain boundaries.

There is a direct important consequence from this for the basic equation: We can replace T(I) by b(I), the set of possible Burgers vectors because they are always translation vectors of the lattice and obtain

(I - A^–1) r₀ = b(I)

Remember that all translations vectors of the lattice are possible Burgers vectors; this came straight from the Volterra definition of dislocations. The fact that observed Burgers vectors are always the smallest possible translation vectors does not interfere with this statement - all it means is that a "Bollmann" dislocation with a large Burgers vector would immediately decompose into several dislocations with smaller vectors.

Our basic equation yields the base vectors of the O-lattice if we feed it with the base vectors, i.e. the smallest possible translation vectors, of the crystal lattice. Since the Burgers vectors in a given lattice are pretty much the smallest possible translation vectors, too, we may see the O-lattice as some kind of transformation of the b-lattice, the lattice defined by taking the permissible Burgers vectors of a crystal as the base vectors of a lattice.

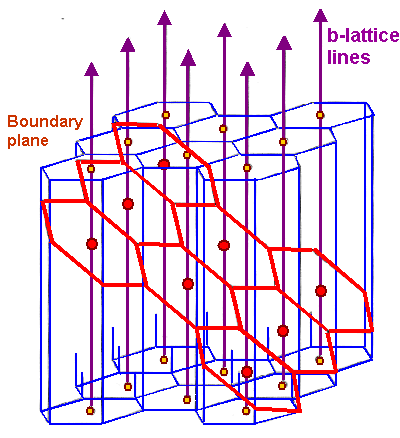
The crucial point now is to realize that the lines of intersection of the the actual plane of the boundary with the cell walls of the O-lattice (which, remember, looks like a honeycomb)), are the dislocations in the grain boundary. Whenever we cross over from one cell in the honeycomb structure to the next, we moved one Burgers vector apart in the real lattices. It is helpful at this point, to study the case of a small angle grain boundary treated in the advanced section under " Bollmanns view of Franks formula"; the essential picture is reproduced below.

The magenta lines are the O-lattice lines; the honeycomb structure is shown in blue, and the intersection with an arbitrary boundary plane produces the red dislocation network.

This is why it becomes important what kind of unit cell we pick for the O-lattice as mentioned before. As always, there are many possible choices.

Bollmann gives precise directions for the choice of the "right" unit cell of the O-lattice - simply take the largest one possible (producing as few dislocations as possible). We will not reproduce the mathematical arguments; here we just note that it is possible to define an optimal O-lattice.

	We now have a big difference in the mental construction of a grain boundary between the O-lattice theory and the CSL theory. From the former we now have a rule for finding the optimal plane of a grain boundary for any given orientation - whereas the CSL model provides this information only for CSL orientations.
		This rule will prove to be very general: We will be able to carry it over to the case of large angle grain boundaries (remember, that all complications notwithstanding, we implicitly deal only with small angle grain boundaries so far).
		We also can obtain quantitative information about the dislocation structure in the chosen plane as long as we we restrict ourselves to small angle grain boundaries.
		In this case the O-lattice theory is just a generalization of Franks formula - all you have to do is to replace "sina" in the transformation matrix by "a" (and use the corresponding linearizations of all other trigonometrical functions for small angles) - Franks formula will result.
	In other words, as long as the spacing of the O-lattice is large compared to the crystal lattices, all of this makes sense, and this condition is always met for small deformations, i.e. for small angle boundaries.
		For O-lattices with lattice constants in the same order of magnitude as the crystals, however, the spacing between the dislocation would be too small as to be physically meaningful - exactly as before. So what is new?
		Well, the O-lattice theory as a generalized version of Franks formula, is not just applicable to small angle grain boundaries, but to "small deformation" boundaries of any kind, including phase boundaries. This is already a remarkable achievement.
		But, as we will see, the complete O-lattice theory also incorporates arbitrary ("large angle") boundaries of all types, too.
	In order to progress, we now must ask the question: Are there any "special" O-lattices, or, in other words, special orientations the crystals would prefer?
		We already know parts of the answer: Yes, there are preferred orientations for grain boundaries; the CSL orientations, which, after all, must also be expressible in the O-lattice concept.
		From this we can go on and this will be dealt with in the next chapter.