|
A perfect dislocation may dissociate into two partial dislocations because this
lowers the total energy. |
|
 |
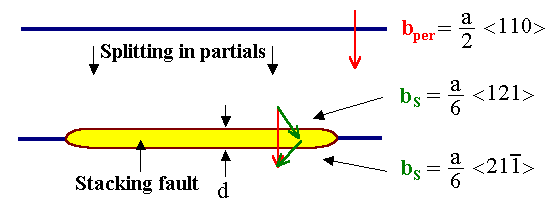
The Burgers vector b = a/2[110] may, e.g., decompose into
the two Shockley partials
a/6[121] and a/6[2,1,–1] as shown below. |
|
 |
Of necessity, a stacking fault between
the two partial dislocations must also be generated. |
|
|
|
|
 |
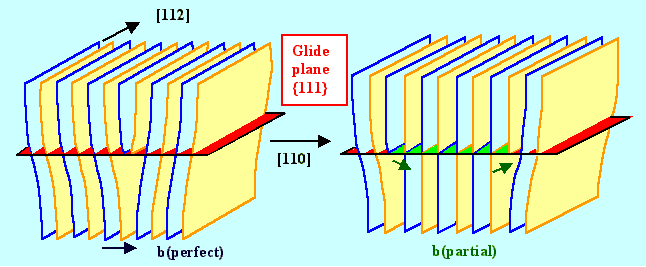
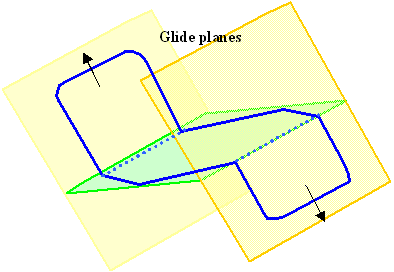
You can think of this as doing two Volterra cuts in the same plane,
each on with the Burgers vector of one of the Shockley partials, but keeping the cut line apart by the distance d.
Each cut by itself makes a stacking fault, but the superposition of both creates a perfect lattice. |
 |
Lets balance the energy of this reaction: |
| |
Energy of the
perfect dislocation |
= G · b2 = G · (a/2<110>)2 |
= | G · a2
2 |
| | |
| |
Energy of the
two partial dislocations |
= 2G · (a/6<112>)2 = 2G
· a2/36 · (12 + 12 + 22) |
= | G · a2
3 |
|
|
|
 |
We thus have a clear energy gain
–Esplit = G · a2 by having smaller Burgers vectors. This energy gain
does not depend on the distance d between the dislocations. |
 |
But we are not done yet; we have two more energy terms to consider: |
|
 |
1. The energy of interaction
+Einter; it will be large at short distances. The dislocations repulse each other and the energy
going with this interaction is proportional to 1/d. Based on this alone,
the partial dislocations thus would tend to maximize d. |
|
 |
2. The energy of the stacking fault
+ESF stretched out by necessity between the two partial dislocations. This stacking fault energy is always ESF = g
· area, or, taken per per unit of length as for the dislocations, E'SF
=g · d. Based on this alone, the partial
dislocations thus would tend to minimize d. |
 |
In total we have some energy gain by just
forming partial dislocations in the first place, but energy losses if we keep them too
close together, or if we move them too far apart. |
 |
We thus must expect that there is an equilibrium distance
deq which gives a minimum energy for the total defect which consists of a split
dislocation and a stacking fault. This equilibrium distance
deq will depend mostly on the stacking fault energy g; for small
g's we expect a larger distance between the partials. |
|
 |
In principle, we can calculate deq by writing down the total energy, i.e. the
sum of the energy gain by forming partial dislocations plus the energy of the interaction plus the stacking fault energy,
then find the minimum with respect to d by differentiation. This is a basic execise, what you will get is
deq µ
g–½ |
 |
Instead of a a pure one-dimensional defect - our perfect dislocation - we have
now something complicated, some kind of ribbon stretching through the crystal. Moreover, this stacking fault ribbon may
be constricted at some knots or jogs, and may look like this: |
|
|
|
 |
How would this look in cross-section? We take a picture after "Hull and Bacon" |
|
|
|
|
 |
It is clear that a dislocation split into Shockley partials is still
able to glide on the same glide plane as the perfect dislocation; the stacking fault just moves along. It can also change
its length without any problems. |
|
 |
For Frank type partials this is not
true. The loop it usually bounds could only move on its glide cylinder.
Changing the length would involve the absorption or emission of point defects. |
 |
Reactions between dislocation now tend to become messy. You must consider the
reaction between the partials and taking into account the stacking fault. However, processes now become possible that could
not have occurred before. Lets look at some examples. |
|
 |
A small dislocation loop formed by the agglomeration of vacancies, that in its pure form cannot add much
to plastic deformation, may transmutate into a dislocation loop bounded by a perfect Burgers vector (which in turn may split
into Shockley partials) - it is now glissile and can increase its length ad libitum. How does that happen? |
|
 |
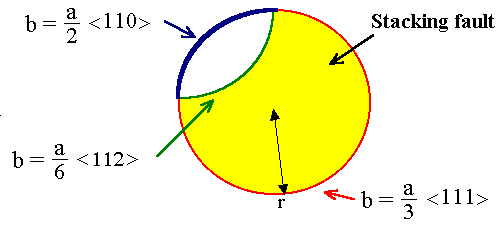
As shown below, the Frank partial bounding the vacancy disc defining the stacking fault
has a Burgers vector of the type b = a/3<111>. It then may split into a perfect dislocation with
b = a/2<110> and a Shockley partial with b = a/6<112> (which must lie in
the loop plane). The Shockley partial moves across the loop, removing the stacking fault - we have an "unfaulting" process. A loop bounded by a perfect dislocation, free to move, is left.
The glide plane of the perfect dislocation is not the plane of the loop; the Burgers vector of the perfect dislocation,
after all, must have a sizeable component perpendicular to the loop plane in order for the sum of the Burgers vectors to
be zero. |
| |
|
|
 |
The Shockley dislocation, once formed, will move quickly over the loop - pulled by the stacking fault like
by a tense rubber sheet. The driving force for the reaction is the stacking fault energy: As the loop increases in size
because more and more vacancies are added and the radius r grows, the energy of the loop increases with r2
due to the stacking fault. However, the line energy of the dislocation only increases with r no matter what
kind of dislocation is bounding the loop. |
|
 |
There is therefore always a critical radius rcrit where a perfect loop becomes
energetically favorable. |
 |
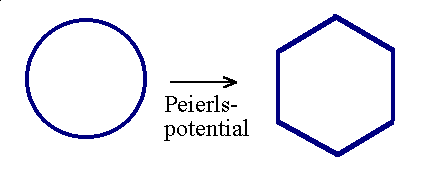
The perfect loop now feels the Peierls potential,
it may try to align the dislocation into the <110> directions, always favorable in fcc lattices the
loop then assumes a hexagonal shape. |
|
|
|
|
 |
Now all segments are able to glide. If the resolved shear stress for some segments is large enough, they
are going to move, pulling out long dislocation dipoles in the direction of the movement. The beginning of this process
may look look this: |
| |
|
 |
What we have, in summary, is one of the problems of Si materials technology:
|
|
 |
We have an efficient source for dislocation generation by vacancy (or, in Si, interstitial)
agglomeration in formerly dislocation free crystals! And this is not a theoretical possibility, but reality if you are not
very careful in growing your crystals. Many examples are shown in the
link. |
| |
|
 |
As we have seen, there are now many possible dislocation reactions. In writing
down reaction equations, you must use the specific Burgers vector (e.g. a/6[1, -2, 1]) and not the general
type (a/6<112> for the example). This can be cumbersome and is prone to produce errors. |
|
 |
Fortunately there is a extremely useful tool for fcc lattices to keep the vectors in
line: The Thompson tetrahedron. |
|
 |
The Thompson tetrahedron is simply the tetrahedron formed by the {111} planes with consistently
indexed planes and edges. |
| |
|
|
 |
If we look at the {111}-planes tetrahedron, we see the following connections
- The edges are <110> directions, they may be used to represent the Burgers
vectors of the perfect dislocations and the preferred direction for the line vectors because of the Peierls potential (red
lines).
- The faces are {111} planes, they show the positions of potential stacking
faults.
- The Burgers vector of the Shockley partials that may bound a stacking fault of the given {111} plane are the
vectors running from the center of the triangular faces to the corners (blue lines)
- The Frank dislocations that also can bound a stacking fault, run from the center of the triangular faces to the center
of the tetrahedron (not shown).
|
|
|
 |
For a "short-hand" description, it is conventional, to enumerate the edges by A,B,C,D
and the centers of their triangles by a, b, g
and d. The relevant vectors than become, e.g., AB or Ag.
|
|
 |
It is a good idea (really!) to really build a Thompson
tetrahedron - maybe from some stiff cardboard; the link gives the detailed
net. |
© H. Föll (Defects - Script)