|
Lomer–Cotrell and stair-rod dislocations |
|
 |
Lets look at the reaction between two perfect dislocations on different glide planes which
are split into Shockley partials, e.g. with the (perfect) Burgers vectors
b1 = a/2[–1,1,0] on the (111) plane
b2 = a/2[101] on the (–1,1,1) plane |
|
 |
If you have not yet produced your personal Thompson
tetrahedra - now is the time you need it! |
|
 |
The two Shockley partials meeting first will always react to form a dislocation with the Burgers vector |
| |
|
|
 |
Use your Thompson tetrahedron to verify this! |
 |
This is a new type of Burgers vector. A dislocation
with this Burges vector is called a Lomer-Cotrell dislocation. |
|
 |
A Lomer-Cotrell dislocation now borders two stacking faults on two
different {111} planes, it is utterly immobile. |
|
 |
The total structure resulting from the reaction - a
Lomer-Cotrell dislocation at the tip of two stacking fault ribbons bordered on the other side by Shockley partials - is
called a stair-rod dislocation because it is reminiscent of the "stair-rod"
that keeps the carpet ribbons in place that are coming down a stair. What it looks like is shown in the link. |
 |
It is clear that this is a reaction that must and will occur during plastic deformation.
Since it makes dislocations completely immobile, it acts as a hardening mechanism;
it makes plastic deformation more difficult. |
 |
Another speciality in fcc-crystals, which would never occur to you by hard
thinking alone, are stacking fault tetrahedra. |
|
 |
Stacking fault tetrahedra are special forms of point defect agglomerates. Lets see what the are and how
they form by again looking at low energy configurations: |
 |
Frank partials bonding a vacancy disc have a rather high energy (b = a/3
[111], b2 = a2/3) compared to a Shockley partial (b2
= a2/6) or Lomer-Cotrell dislocation (b2 = a2/18), which also
can bound stacking faults. Is there a possibility to change the dislocation type? |
|
 |
There is! Imagine the primary stacking fault to be triangular. Let the Frank partial dissociate into a
Lomer-Cotrell dislocation and a Shockley partial which can move on one of the other {111}-planes intersecting the
edge of the triangular primary stacking faults. (If you do not have a Thompson tetrahedra by now, it serves you right!) |
|
 |
Let the Shockley partials move; wherever they meet they form another Lomer-Cotrell dislocation. If you
keep them on other triangular areas, they will finally meet at one point - you have a tetrahedron
formed by stacking faults and bound by Lomer-Cotrell dislocations; the whole process is shown in the link. |
|
 |
If this seems somewhat outlandish, look at the electron
microscopy pictures in the link! |
 |
Next, lets look at slightly more complicated fcc-crystals: the diamond structure typical not only for diamond, but especially for Si, Ge,
GaAs, GaP, InP, ... Now we have two atoms in the base of the crystal,
which makes things a bit more complicated. |
|
 |
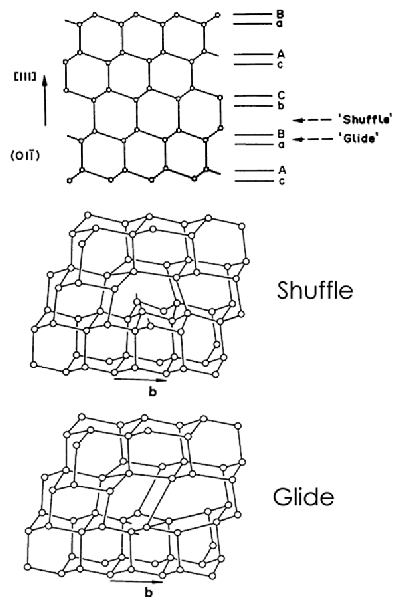
First of all, the extra lattice plane defining an edge dislocation may now come in two
modifications called "glide"- and "shuffle"
set, because the inserted half-plane may end in two distinct atomic positions as shown below. The properties of
dislocations in semiconductors - not only their mobility but especially their possible states in the bandgap - must depend
on the configuration chosen. |
| |
|
|
 |
Which configuration is the one chosen by the crystal? It is still not really clear and a matter of current
research. |
| |
|
|
Some
Specialities in bcc Lattices |
| |
|
 |
The basic geometry in bcc lattices is more complicated, because it is not
a close-packed lattice. |
|
 |
The smallest possible perfect Burgers vector is |
| |
|
|
 |
Glide planes are usually the most densely packed planes, but in contrast to the fcc lattice, where
the {111} planes are by far most densely packed, we have several
planes with very similar packing density in bcc crystals, namely {111}, {112} and {123}.
|
|
 |
This offers many possibilities for glide systems, i.e. the combinations
of possible Burgers vectors and glide planes. Segments of dislocations, if trapped on one plane may simply change the plane
(after re-aligning the line vector in the planes). |
|
 |
Stacking faults (and split dislocations) are not observed because the stacking fault energies are too large. |
|
 |
But the core of the dislocations, especially for screw dislocations, can now be extended and rather complicated.
Screw dislocations in <111> directions, e.g., have a core with a threefold symmetry. This leads to a basic
asymmetry between the forward and backward movement of a dislocation: |
| |
|
|
 |
Imagine an oscillating force acting on a bcc metal - Fe for that matter. The
screw dislocation will follow the stress and oscillate between two bowed out positions. As long as the maximum stresses
are small compared to the critical stress needed to induce large scale movement, the process should be completely reversible. |
 |
However, due to the asymmetry between forwards and backwards movement, there is a certain
probability that once in a while the screw dislocation switches glide planes. It then may move for a large distance, inducing
some deformation, In due time, things change irreversibly leading to a sudden failure called "fatigue".
|
 |
This is only one mechanism for fatigue and only serves
to demonstrate the basic concept of long-time changes in materials under load due to details in the dislocation structure
of materials. |
|
| |
© H. Föll (Defects - Script)