| fcc | bcc | hcp | |||||
|---|---|---|---|---|---|---|---|
| Dichtest gepackte Ebenen |
{111} 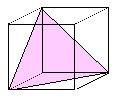 | {110}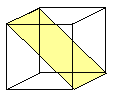 | a- Fe, W, Mo, b-Messing | {0001}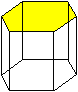 |
Cd, Zn, Mg, Be, Al2O3 | ||
{211}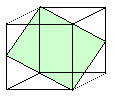 | a- Fe, W, Mo, Na | {10–10}  | Ti, Zr | ||||
{321} | a- Fe, K | {10–11}  | Ti, Mg (selten) | ||||
| Bemerkungen | Keine anderen Ebenen haben ähnlich hohe Packungsdichten. |
Die {110} Ebene ist zwar am dichtesten gepackt, aber die beiden anderen sind ähnlich. Die {211} Ebene enthält Stapelfehler (falls vorhanden). Alle Ebenen enthalten den <111> Typ Burgersvektor |
Man spricht von "Basis"-, "Prismen"- und "Pyramiden"gleitung . Ohne Gleitung auf einer Nicht-Basisebene keine allgemeine Verformung! | ||||
| Anzahl | 4 (111), (-111), (1-11), (-1-11) |
{110}: 6 {211}: 12 {321}: 24 |
{0001}: 1 {10–10}: 3 {10–11}: 6 |
||||
| Kürzest- möglicher b Vektor |
a/2<110> | a/2<111| | 1/3<11–20> | ||||
| Anzahl pro Gleitebene | 3 Auf (111): a/2[110], | {110}: 2 {211}: 1 {321}: 1 |
{0001}: 3 {10–10}: 1 {10–11}: 1 |
||||
| Anzahl Gleitsysteme |
12 (= 3 · 4) | {110}: 12 = 6 · 2 {211}: 12 = 12 · 1 {321}: 24 = 24 · 1 |
{0001}: 3 = 1 · 3 {10–10}: 3 = 3 · 1 {10–11}: 6 = 6 · 1 | ||||