Figure 4.6:
Momentum (speed) distribution in \(z\) direction between two walls of different
speed in \(x\) direction.
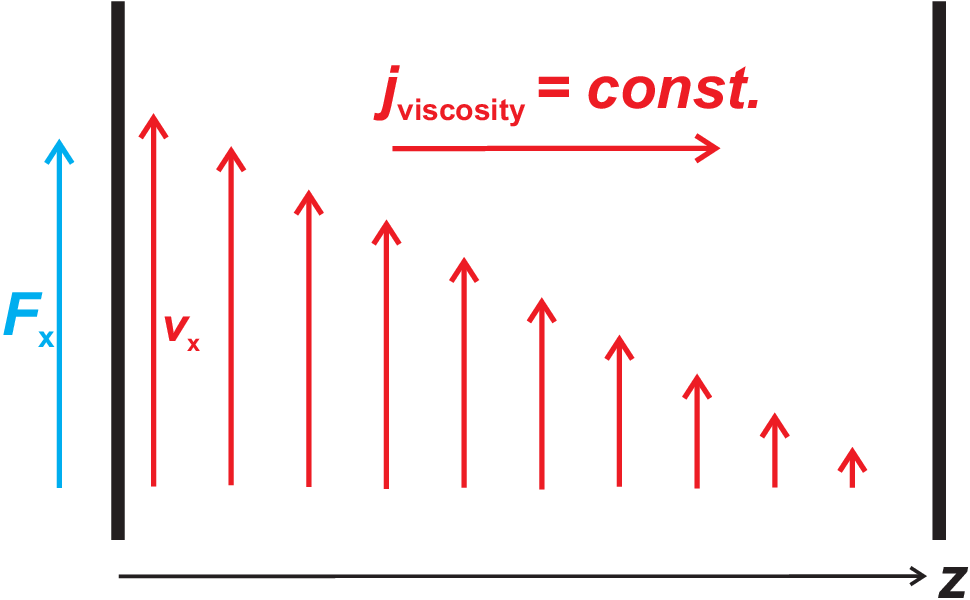
The standard definition of viscosity is illustrated in Fig. (4.6). One wall is moving in \(z\)-direction with speed \(v_z\), induced by a force \(F_z\). The second wall is fix. A linear reduction of speed \(v_z\) of the viscous liquid is observed implying a momentum current density flowing from left to right.
Experimentally a relation between force \(F_z\) and velocity \(v_z\) in z-direction is found to be
|
| \begin{equation*} F_x = \eta A \frac{v_x}{z} \quad , \label{large_visc} \end{equation*} | (4.70) |
where \(A\) is the cross section, \(x\) the distance between the two walls, and the viscosity \(\eta\) is a linear scaling factor. For small distances \(z\) the Eq. (4.70) translates into
|
| \begin{equation*} F_x = \eta A \frac{\partial v_x}{\partial z} \quad , \label{small_visc} \end{equation*} | (4.71) |
giving rise to the precise definition of the viscosity \(\eta\). The linear reduction of \(v_x\) in z-direction can easily be understood from the continuity equation (4.57) which for the above case (and adding sources and drains) reads
|
| \begin{equation*} \frac{\partial (\rho v_z)}{\partial t} = - \frac{\partial j_{viscosity}}{\partial z} \mbox{+ sources - drains .} \label{visc_cont} \end{equation*} | (4.72) |
here \(\rho = m / V\) is the mass density.
Temporal changes
of momentum are induced by forces; so possible sources and drains in Eq. (4.72) are additional forces. Since no such forces are applied we find for steady state, i.e. \(\partial (\rho v_x) / \partial t = 0\),
|
| \begin{equation*} 0 = \frac{\partial j_{viscosity}}{\partial z} \quad \text{, i.e.} \quad j_{viscosity} = const. \label{visc_linear} \end{equation*} | (4.73) |
So exactly as for diffusion in Eq. (4.56) a linear relation is found for which the continuity equation is the underlying reason.
 |
 |
 |
 |
© J. Carstensen (TD Kin II)