Figure 4.5:
Gauss bell-shaped curve for several variances \(\sigma\).
The solution of a differential equation of course depends decisively on the boundary conditions which for the example of the diffusion equation are the starting as well as the spatial boundary condition. Here we will discuss the diffusion of a limited point source within an infinitely large 1D tube. The general solution is
|
| \begin{equation*} c(t,x) = \frac{C}{\sqrt{t}} e^{-x^2/ 4Dt} \quad \mbox{where} \quad C = const. \end{equation*} | (4.64) |
The over all particle number ”\(n\)” is fix, i.e.
|
| \begin{equation*} n = \int_{-\infty}^{+\infty} \frac{C}{\sqrt{t}} e^{-x^2/ 4Dt} = \frac{C}{\sqrt{t}} \frac{\sqrt{\pi}}{\frac{1}{\sqrt{4Dt}}} \quad , \end{equation*} | (4.65) |
leading to
|
| \begin{equation*} C = \frac{n}{2\sqrt{\pi D}} \quad \Rightarrow \quad c(t,x) = \frac{n}{2\sqrt{\pi D t}} e^{-x^2/ 4Dt} \quad . \end{equation*} | (4.66) |
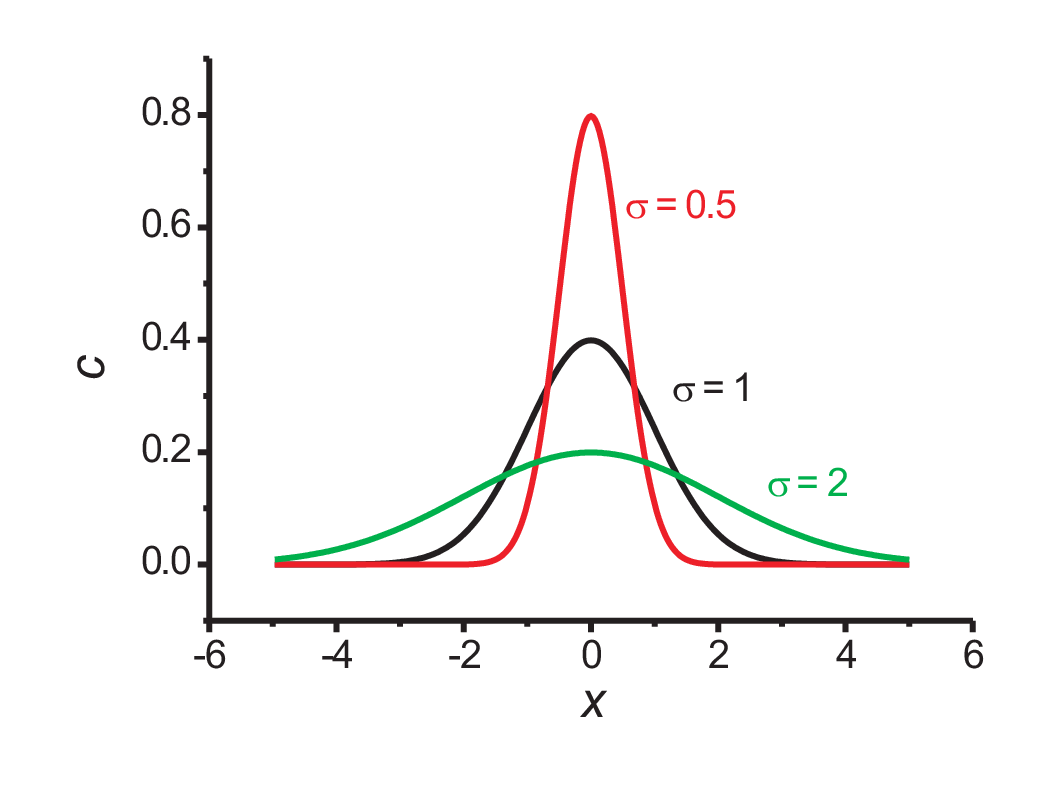
So the solution is a Gauss bell-shaped curve with a variance \(\sigma^2 = 2 D t\), increasing linearly with time \(t\).
This behavior is illustrated in Fig. 4.5 which shows a Gauss bell-shaped curve for three different variances \(\sigma\). The mean square distance traveled by one particle along \(\pm x\) is
|
| \begin{equation*} \overline{x^2} = \frac{1}{n} \int_{-\infty}^{+\infty} x^2 \frac{n}{2\sqrt{\pi D t}} e^{-x^2/ 4Dt} dx = 2 D t\quad . \end{equation*} | (4.67) |
Correspondingly we find for the mean square distance traveled by a particle in 3D
|
| \begin{equation*} \overline{r^2} = \overline{x^2 + y^2 + z^2} = \overline{x^2} + \overline{y^2} + \overline{z^2} = 6 D t \quad . \end{equation*} | (4.68) |
The mean distance traveled by a particle in \(+x\) direction is
|
| \begin{equation*} \overline{x} = \frac{1}{2\sqrt{\pi D t}} \int_{0}^{+\infty} x e^{-x^2/ 4Dt} dx = 2 \sqrt{\frac{D t}{\pi}}\quad . \end{equation*} | (4.69) |
 |
 |
 |
 |
© J. Carstensen (TD Kin II)