Laminar flow through a round tube: Poiseuille’s formula

4.10 Laminar flow through a round tube: Poiseuille’s formula

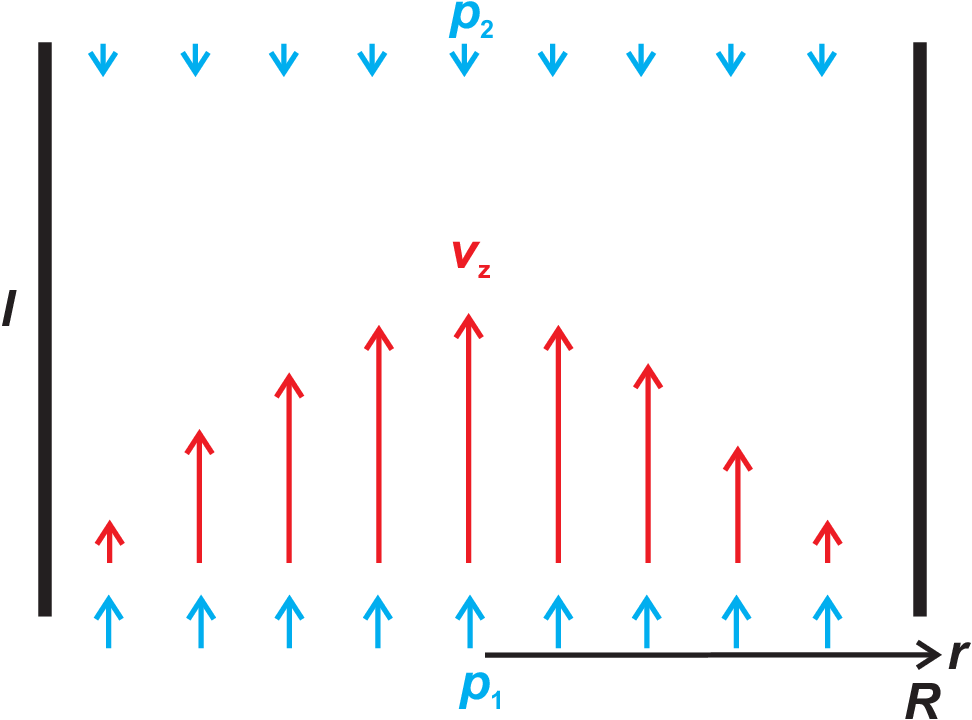
Here we will discuss the laminar flow of a liquid through a straight tube (length \(l\)) showing a round cross section with radius \(R\) (cf. Fig. (4.7)). Liquid flow through the tube is enforced by a pressure difference \(p_2 - p_1\). Friction within the liquid is described by the viscosity \(\eta\). Due to the radial symmetry of the tube the flow pattern can only show a dependence on the position \(r\) (distance from the center of the tube). Exactly this is meant by ”laminar”, in contrast to ”turbulent” where curls within the flow pattern exist.

Figure 4.7: Momentum (speed) distribution in \(x\) direction between two walls of different speed in \(z\) direction.

The pressure force action on the outer surface of the liquid is

\begin{equation*} F_p = \pi r^2 (p_1 - p_2) \quad . \end{equation*}

(4.74)

The friction force acting on an inner cylindrical surface \(2 \pi r l\) is

\begin{equation*} F_r = 2 \pi r l \eta \frac{dv}{dr} \quad . \end{equation*}

(4.75)

In steady state both forces compensate for each other, i.e. \(F_r + F_p = 0\), leading to

\begin{equation*} \frac{dv}{dr} = \frac{\pi r^2 (p_2 - p_1)}{2 \pi r l \eta} = \frac{r}{2\eta} \frac{p_2 - p_1}{l}\quad , \end{equation*}

(4.76)

which after integration gives

\begin{equation*} v(r) = \frac{r^2}{4 \eta} \frac{p_2 - p_1}{l} + C\quad . \end{equation*}

(4.77)

Due to the sticking at the surface \(v(R) = 0\) holds, so

\begin{equation*} C = - \frac{R^2}{4 \eta} \frac{p_2 - p_1}{l} \quad , \end{equation*}

(4.78)

finally giving

\begin{equation*} v(r) = \frac{R^2-r^2}{4 \eta} \frac{p_1 - p_2}{l}\quad . \end{equation*}

(4.79)

The flow pattern thus is a paraboloid.
The liquid volume flowing per time \(t\) through the hollow cylinder between \(r\) and \(r+ dr\) is

\begin{equation*} d V = 2 \pi r dr v(r) t \quad . \end{equation*}

(4.80)

and thus through the whole tube

\begin{equation*} \begin{split} V & = \int_0^R 2 \pi r dr v(r) t \\ & = 2 \pi t \frac{p_1 - p_2}{4 \eta l} \int_0^R r dr (R^2-r^2) = \pi t \frac{p_1 - p_2}{8 \eta l} R^4 \quad , \end{split} \end{equation*}

(4.81)

leading to a liquid flow

\begin{equation*} \frac{V}{t} = \pi \frac{p_1 - p_2}{8 \eta l} R^4 \quad , \end{equation*}

(4.82)

which is Poiseuille’s formula: applying the same pressure difference but halving the radius of the tube the flow reduces by a factor of 16. This tremendous effect of reducing the radius of a tube has to be taken into account, e.g. when designing small liquid flow systems or discussing micro-fluidity.