Figure 4.4:
a) General model for describing continuity in transport phenomena. b) Diffusion generally levels
out concentration gradients.
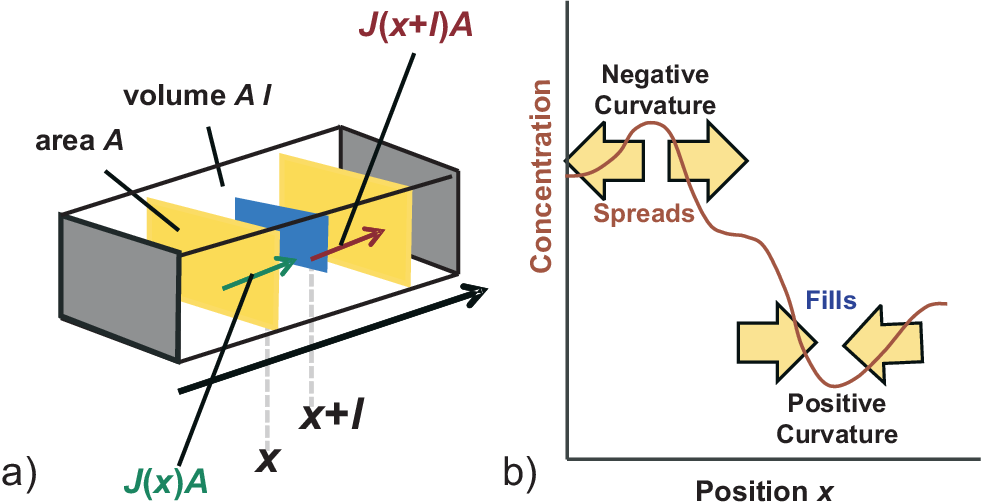
In this section we will discuss time dependencies, e.g. how long it takes to reach steady state or thermodynamic equilibrium. For this we will allow the concentration \(c\) to change at any point. Such local concentration changes are induced by lateral current flow and/or local sources or drains. First we discuss changes of the local concentration \(c\) as a function of time just induced by local current densities. This is illustrated in Fig. 4.4 a) for the change of concentration \(c\) in a (tiny) volume \(A l\) induced by a difference of current flowing into and out of this volume in \(x\) direction, i.e. in a 1D model. The number of particles entering the volume at position \(x\) per time \(dt\) is
|
| \begin{equation*} dn^{in} = j(x) A dt \quad . \end{equation*} | (4.52) |
Correspondingly the number of particles leaving the volume at position \(x+l\) per time \(dt\) is
|
| \begin{equation*} dn^{out} = j(x+l) A dt \quad . \end{equation*} | (4.53) |
Thus the change of concentration in the volume \(A l\) per time \(dt\) is
Here we just used that for small \(l\) the linear order of the Taylor expansion is enough to describe the changes of \(j(x+l)\). Eq. (4.54) is the continuity equation in 1D. Combining it with the equation for diffusion current (cf. Eq. (4.42)) we get the one dimensional diffusion equation
|
| \begin{equation*} \frac{dc}{dt} = D \frac{d^2 c}{dx^2} \quad . \label{diff_eq_1D} \end{equation*} | (4.55) |
As illustrated in Fig. 4.4 b) diffusion reduces curvatures (”Nature abhors a wrinkle”):
Negative curvature: decrease of \(c(t)\).
Positive curvature: increase of \(c(t)\).
In steady state, i.e. stationary condition, we have
|
| \begin{equation*} \frac{dc}{dt} = 0 \quad \Rightarrow \quad \frac{d c}{dx} = const. \quad . \label{diff_eq_1D_steady_state} \end{equation*} | (4.56) |
Without sources and drains at the surface we find \(\frac{d c}{dx} = 0\) which describes thermodynamic equilibrium.
The generalization of the 1D version of the continuity equation Eq. (4.54) is straight forward since in general the gradients in \(y\) and \(z\) direction can contribute to the change of the local concentration as well, leading to
|
| \begin{equation*} \frac{dc}{dt} = - \frac{dj_x}{dx} - \frac{dj_y}{dy} - \frac{dj_z}{dz} = - \vec{\nabla} \vec{j} = - \,\mbox{div}\; \vec{j} \quad , \label{cont_eq_3D} \end{equation*} | (4.57) |
which is the continuity equation in 3D.
Taking the 3D version of the diffusion equation as introduced in Eq. (4.42)
|
| \begin{equation*} \vec{j} = - D \vec{\nabla} c = - D \; \mbox{grad}\; c \quad , \label{diff_curr_3D} \end{equation*} | (4.58) |
and combining it with Eq. (4.57) we get the diffusion equation
|
| \begin{equation*} \frac{dc}{dt} = D \vec{\nabla} \vec{\nabla} c = D \; \mbox{div grad}\; c = D \Delta c \quad . \label{diff_eq_3D} \end{equation*} | (4.59) |
 |
 |
 |
 |
© J. Carstensen (TD Kin II)