Figure 4.3:
a) Geometry of the collision tube. b) Momentum distribution close to a wall allowing for the
definition of viscosity. c) General model for describing transport phenomena.
Scattering is the essential concept to understand
transport phenomena in vapors, liquids, and solids. Without scattering all particles would keep their velocity even without
any external force which of course is experimentally only found under vacuum condition. Typically moving particles with
a density \(n\) are scattered by (non moving) particles (defects) with a density \(N\). One possible
fundamental error being related to scattering is the expectation that a mean free path \(\lambda\) between
two scattering events of the moving particles is related to the mean distance between defects. This would in 3D imply that
\(\lambda \propto N^{1/3}\) which is in contradiction to the experimental finding \(\lambda \propto
N\). The correct modeling needs for the concept of a collision/scattering cross section \(\sigma\). This concept
has first been introduced and can most easily be understood for a perfect gas where the moving particles and the scatter
centers are the same gas molecules. On the one hand the perfect gas allows for a very easy and illustrative understanding
of the collision cross section area, on the other hand that both scattering partners are moving implies an additional complexity
to the problem. So in what follows we will discuss both examples in parallel.
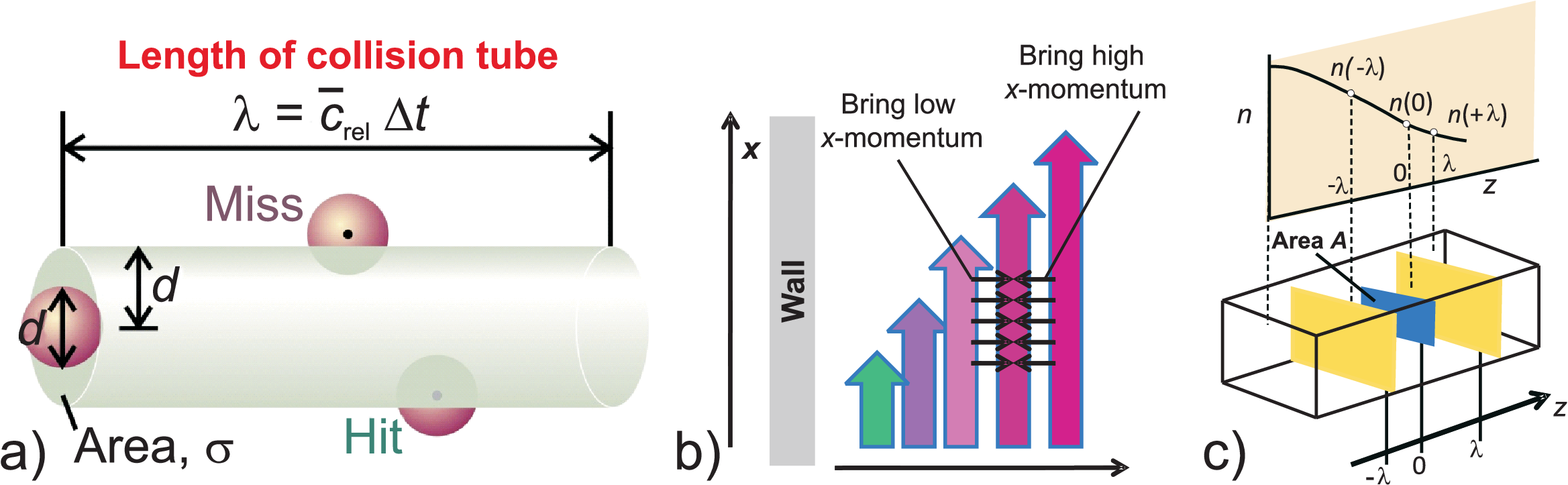
As illustrated in Fig. 4.3 a) the starting point of the discussion of scattering
of gas molecules is a frozen state model, i.e. all particles except one are assumed to stay fix while one particle
is moving down the collision tube. Just geometrically a collision cross section \(\sigma\) is defined:
|
| \begin{equation*} \sigma = \pi \left(r_1 + r_2 \right)^2 \approx \pi \left(2 r_1\right)^2 = \pi d^2 \quad \mbox{for} \quad r_1 \approx r_2 \quad . \end{equation*} | (4.34) |
For classical particles (gas molecules) the size of the diameter \(d\) of
a collision tube is quite easy to understand and well determined, but e.g. for
electrons within a metal ”colliding” with defects the electron scattering cross section is more a fitting parameter
quantifying the relevance of defects as scattering centers.
Introducing the volume of the collision
tube \(V_{ct}\) and using the particle density \(n^*\) the
mean free path \(\lambda\) is calculated by
|
| \begin{equation*} \lambda \sigma = V_{ct} = \frac{1}{n^*} \quad \mbox{i.e.} \quad \lambda = \frac{1}{\sigma \; n^*} \quad . \end{equation*} | (4.35) |
Introducing the average time between two collisions \(\Delta t\) and the average relative speed between particles \(\overline{c}_{rel}\) we get \(\Delta t= \lambda / \overline{c}_{rel}\) which allows us to calculate the number of collisions inside the collision tube per time by
|
| \begin{equation*} z = \frac{1}{\Delta t} = \frac{V_{ct} n^*}{\Delta t} = \frac{\sigma \overline{c}_{rel} \Delta t n^*}{\Delta t} = \sigma \overline{c}_{rel} n^* \quad . \end{equation*} | (4.36) |
For e.g. electrons and typical defects \(\overline{c}_{rel} = \overline{c}\) is just the average speed of the electrons which can be calculated using various models, \(n^* = N\) is the defect density, and \(\sigma\) a parameter depending on the type of defects and the type of metal.
For a perfect gases \(n^* = p / kT\) and \(\overline{c}_{rel} = \sqrt{2} \overline{c}\) (According to Eq. (4.23) the factor \(\sqrt{2}\) shows up from a non trivial averaging procedure and will not be discussed here in more detail), so
|
| \begin{equation*} z = \frac{\sqrt{2} p \,\sigma\,\overline{c}}{kT} \quad , \end{equation*} | (4.37) |
which e.g. for \(N_2\) at 300 K and 1 bar (\(M = 28 \, g/mol\)) leads to
|
| \begin{equation*} \overline{c}= \sqrt{\frac{8RT}{\pi M}} \approx 476 \, m / s \quad ; \quad z \approx 7 \times 10^9 s^{-1} \quad , \end{equation*} | (4.38) |
so the time between two collisions is \(1/z = 1.4 \times 10^{-10} s\).
The mean free path \(\lambda\), i.e. the average distance that particles can travel between two collisions, is
|
| \begin{equation*} \lambda = \overline{c} \frac{1}{z} = \frac{1}{\sqrt{2}\sigma n^*} = \frac{kT}{\sqrt{2} p \sigma} \quad , \label{mean_free_path} \end{equation*} | (4.39) |
which for the example of \(N_2\) above results in \(\lambda \approx 68 \, nm\).
Each moving particle transports several other properties like it’s charge, energy,
momentum, or mass. Having thermodynamic equilibrium on average for each particle moving in one direction one particle is
found moving in the opposite direction, so no net transport exists. Introducing forces/reservoirs which continuously sustain
gradients in certain properties net transport will occur; thus we leave the regime of thermodynamic equilibrium and discuss
kinetics.
The following model is quite general. We will discuss the transport
of the property \(\Gamma\) by moving particles with a density \(n^*\) and a velocity \(v\) which by collision transfer \(\Gamma\) to other particles.
Such collisions will on average occur when particles have traveled a mean free path \(\lambda\). As the only
relevant simplification we assume that the lateral changes in the parameter \(\Gamma\), \(n^*\),
and \(v\) are of linear order on the length scale of \(\lambda\), i.e. a Taylor expansion
up to linear order is suitable to calculate net transport of \(\Gamma\). Schematically this conditions are
shown in Fig. 4.3 c), and Fig. 4.3 b) illustrates the situation used for describing
viscosity, i.e. \(\Gamma\) being the momentum in \(x\) direction with gradients in \(z\) direction.
Let us discuss the situation at an arbitrary position \(z_1\).
From the right side a particle flow will collide at position \(z_1\) coming on average from \(z_1+\lambda\),
i.e.
Correspondingly from the left side we find
We will use the above relations to find the corresponding microscopic descriptions for transport of matter (diffusion), energy (heat transport), and momentum (viscosity)
|
| \begin{equation*} j_{diff}= - D \frac{dn}{dz} \quad j_{heat}= - \kappa \frac{dT}{dz} \quad j_{viscosity}= - \eta \frac{dv_x}{dz} \quad . \label{currents_1D} \end{equation*} | (4.42) |
Just for simplicity we restrict the notation to 1 D and will later (easily) translate to
a 3D notation.
The difference between both particle flows in Eq. (4.40) and Eq. (4.41) is already
one of the fundamental transport mechanisms. Having \(v= const. = \overline{c}\) (i.e. \(T
= const.\)) we find
|
| \begin{equation*} - \frac{1}{3} \lambda \overline{c} \frac{dn}{dx} := - D \frac{dn}{dx} = j_{diff} \qquad \mbox{, i.e.} \qquad D = \frac{1}{3} \lambda \overline{c} \quad . \end{equation*} | (4.43) |
For viscosity \(n\) and \(v\)
and the variation of \(v_x\) in \(z\) direction is illustrated in Fig. 4.3. Only the transported momentum in \(x\) direction
differs along the \(z\)-direction:
From right:
|
| \begin{equation*} - \frac{1}{6} n^* v m \left[v_x + \lambda \frac{dv_x}{dz} \right] \quad . \end{equation*} | (4.44) |
From left:
|
| \begin{equation*} + \frac{1}{6} n^* v m \left[v_x - \lambda \frac{dv_x}{dz} \right] \quad , \end{equation*} | (4.45) |
leading to the difference
|
| \begin{equation*} -\frac{1}{3} n^* v m \lambda \frac{dv_x}{dz} \quad \mbox{, i.e.} \quad \eta = \frac{1}{3} n^* m v \lambda \quad. \end{equation*} | (4.46) |
For gases the viscosity is independent of the pressure since according to Eq. (4.39) the product \(\lambda n^* =
const.\).
Since \(v \propto T\) the viscosity of gases increases with increasing temperature.
In contrast for liquids the viscosity decreases with increasing temperature, following a law \(\eta = A e^{b/T}\). This can be explained by a necessary activation energy for a sliding of molecule layers against each other.
Having temperature gradients within gases each particle transports heat energy \(\frac{1}{2}
m \overline{v^2} = \frac{f}{2} k T\). The heat currents are
From right:
|
| \begin{equation*} \frac{1}{6} n^*(z_1+\lambda) \left(\overline{v} + \lambda \frac{dv}{dz}\right) \frac{f}{2} k T(z_1+\lambda)\quad . \end{equation*} | (4.47) |
From left:
|
| \begin{equation*} - \frac{1}{6} n^*(z_1-\lambda) \left(\overline{v} - \lambda \frac{dv}{dz}\right) \frac{f}{2} k T(z_1-\lambda)\quad . \end{equation*} | (4.48) |
Since \(p\) is constant (i.e. isobaric condition), according to the ideal gas equation we find \(const.=p= k T N/V = k T n^*\), so only the change in velocity is relevant leading to the difference
|
| \begin{equation*} -\frac{1}{3} n^* \frac{f}{2} k T \lambda \frac{d\overline{v}}{dz} \quad. \end{equation*} | (4.49) |
Since \(T \propto \overline{v}^2\) we get
|
| \begin{equation*} \frac{1}{\overline{v}}\frac{d\overline{v}}{dz} = \frac{1}{2}\frac{1}{T}\frac{dT}{dz} \quad, \end{equation*} | (4.50) |
finally leading to a heat current
|
| \begin{equation*} j = -\frac{1}{3} n^* \frac{f}{2} k \overline{v} \lambda \frac{dT}{dz} \quad \mbox{, i.e.} \quad \kappa = \frac{f}{6} n^* k \overline{v} \lambda \end{equation*} | (4.51) |
 |
 |
 |
 |
© J. Carstensen (TD Kin II)