Special speed values for Maxwell distribution

4.3 Special speed values for Maxwell distribution

Special values for speed can be calculated for the Maxwell distribution

Mean speed

\begin{equation*} \overline{v} = \overline{c} = \int_0^\infty v f(v) dv = 4 \pi \left(\frac{M}{2\pi RT} \right) \int_0^\infty v^3 e^{-\frac{M v^2}{2RT}} dv = \sqrt{\frac{8 R T}{\pi M}} \quad . \end{equation*}

(4.20)

Mean square speed

\begin{equation*} \overline{v^2} = \overline{c^2} = \int_0^\infty v^2 f(v) dv = 4 \pi \left(\frac{M}{2\pi RT} \right) \int_0^\infty v^4 e^{-\frac{M v^2}{2RT}} dv = \frac{3 R T}{M} \quad \Rightarrow \quad c = \sqrt{ \frac{3 R T}{M}} \quad . \end{equation*}

(4.21)

Most probable speed

\begin{equation*} \frac{df(v)}{dv} = 0 \quad \Rightarrow v_{max} = c^* = \sqrt{ \frac{2 R T}{M}} \quad . \end{equation*} (4.22)
Since within the ensemble all particles move one can define the relative mean speed of two distinct particles (which depends mainly on the masses of the particles)

\begin{equation*} \overline{c}_{rel} = \sqrt{\frac{8 R T}{\pi \mu}} \quad \mbox{, with} \quad \mu = \frac{M_A \, M_B}{M_A + M_B} \quad , \label{Eq_relspeed} \end{equation*} (4.23)

which for the special case of identical particles (same masses) translates into

\begin{equation*} \overline{c}_{rel} = \sqrt{\frac{8 * 2 R T}{\pi M}} = 4 \sqrt{\frac{R T}{\pi M}} \quad . \end{equation*} (4.24)

Figure 4.2: a) Principle curve of the Maxwell speed distribution. b) Selector setup the measure speed distributions.

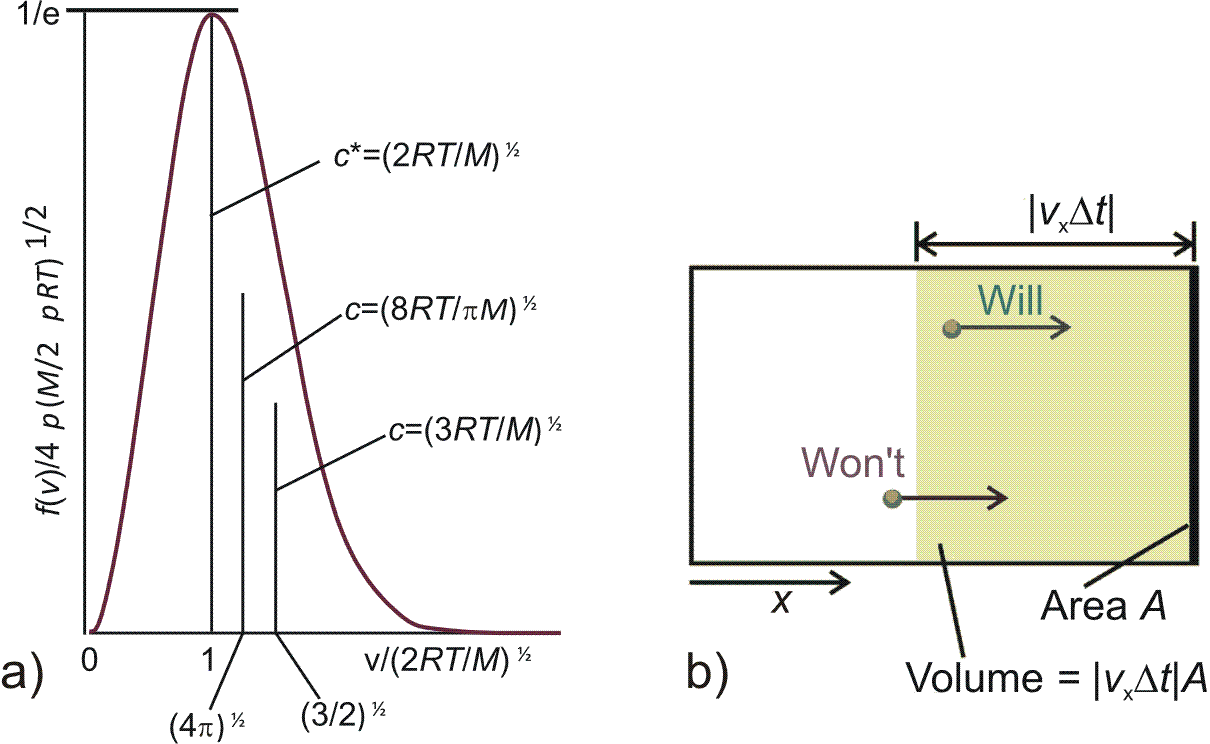
These special speed values are shown in Fig. 4.2 a).
In addition Fig. 4.2 b) illustrates the number of particles \(N_P\) with speed \([v_x, v_x + dv_x]\), \([v_y, v_y + dv_y]\), \([v_z, v_z + dv_z]\) that will collide with the container wall within the period \(\Delta t\)

\begin{equation*} N_P = n^* A v_x \Delta t f(v_x, v_y, v_z) dv_x dv_y dv_z \quad . \end{equation*}

(4.25)

So the pressure applied to the container wall is

\begin{equation*} \begin{split} p_{\Delta t} & = \frac{2 m}{A \Delta t} \sum_j v_{x j} \equiv p = \frac{2 m}{A \Delta t} \left(N_P \overline{v_x}\right)\\ & = \frac{2 m}{A \Delta t} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \int_{0}^{+\infty} n^* A v_x^2 \Delta t f(v_x, v_y,v_z) dv_x dv_y dv_z\\ & = 2 n^* m \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \int_{0}^{+\infty} v_x^2 f(v_x, v_y,v_z) dv_x dv_y dv_z\\ & \qquad \qquad \qquad \qquad \qquad \mbox{(only particles approaching the wall count)}\\ & = n^* m \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} v_x^2 f(v_x, v_y,v_z) dv_x dv_y dv_z\\ & = n^* m \overline{v_x^2} = \frac{1}{3} n^* m \overline{v^2} \quad \mbox{ since } \quad \overline{v_x^2} = \overline{v_y^2} = \overline{v_z^2} = \frac{1}{3} \overline{v^2} \quad . \end{split} \label{p_1} \end{equation*}

(4.26)

Taking once more into account the equipartition law (temperature of the sample correlates with the average kinetic energy of the particles)

\begin{equation*} \overline{E_{kin}} = \frac{1}{2} m \overline{v^2} = \frac{3}{2} k T \quad , \end{equation*}

(4.27)

the final result of Eq. (4.26) can be rewritten as

\begin{equation*} p = \frac{1}{3} n^* m \overline{v^2} = \frac{2}{3} \frac{N}{V} \overline{E_{kin}} = \frac{N k T}{V} \quad , \label{p_2} \end{equation*}

(4.28)

which is just the ideal gas equation.