Distribution of speeds

4.2 Distribution of speeds

Since we talk about classical particles and as will in details be discussed in the next chapter the speed distribution function is up to a constant the Boltzmann factor, i.e.

\begin{equation*} f(v_x, v_y, v_z) = A e^{-\frac{m\left(v_x^2 + v_y^2 + v_z^2 \right)}{2 k T}} = A e^{-B\left(v_x^2 + v_y^2 + v_z^2 \right)} \quad \mbox{with} \quad B = \frac{m}{2 k T} \quad , \end{equation*}

(4.12)

thus

\begin{equation*} \begin{split} 1 & = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(v_x, v_y, v_z) dv_x dv_y dv_z \\ & = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(v_x) f(v_y) f(v_z) dv_x dv_y dv_z \\ & = A \int_{-\infty}^{+\infty}e^{-B v_x^2} dv_x \int_{-\infty}^{+\infty}e^{-B v_y^2} dv_y \int_{-\infty}^{+\infty}e^{-B v_z^2} dv_z \\ & = A \left(\frac{\pi}{B} \right)^{3/2} \quad \Rightarrow \quad A = \left(\frac{B}{\pi} \right)^{3/2} = \left(\frac{m}{2 \pi kT} \right)^{3/2}\quad . \end{split} \end{equation*}

(4.13)

So for the mean square speed we find

\begin{equation*} \begin{split} \overline{v_x^2} & = A \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} v_x^2 e^{-B \left(v_x^2+v_y^2+v_z^2\right)} dv_x dv_y dv_z \\ & = A \left(\frac{\pi}{B} \right) \int_{-\infty}^{+\infty} v_x^2 e^{-B v_x^2} dv_x \\ & = A \left(\frac{\pi}{B} \right) \frac{1}{2} \sqrt{\frac{\pi}{B^3}} = \frac{A}{2 B} \left(\frac{\pi}{B} \right)^{3/2} = \frac{kT}{m} \quad , \end{split} \end{equation*}

(4.14)

leading to the well known result from equipartition law

\begin{equation*} \frac{m}{2} \overline{v_x^2}= \frac{k T}{2} \quad . \end{equation*}

(4.15)

In summary, for the 3D case we get

\begin{equation*} f(v_x, v_y, v_z) = \left( \frac{m}{2 \pi k T}\right)^{3/2} e^{-\frac{m}{2 k T} \left(v_x^2 + v_y^2 + v_z^2 \right)} \quad . \end{equation*}

(4.16)

Assuming isotropy, for the 1D case we find

\begin{equation*} f(v_x) = \left( \frac{m}{2 \pi k T}\right)^{1/2} e^{-\frac{m}{2 k T} v_x^2} \quad , \end{equation*}

(4.17)

and for the norm of the velocity \(v\) we find with \(dv_x dv_y dv_z = 4 \pi v^2 dv\)

\begin{equation*} f(v) = 4 \pi v^2 \left( \frac{m}{2 \pi k T}\right)^{3/2} e^{-\frac{m v^2}{2 k T}} \quad , \end{equation*}

(4.18)

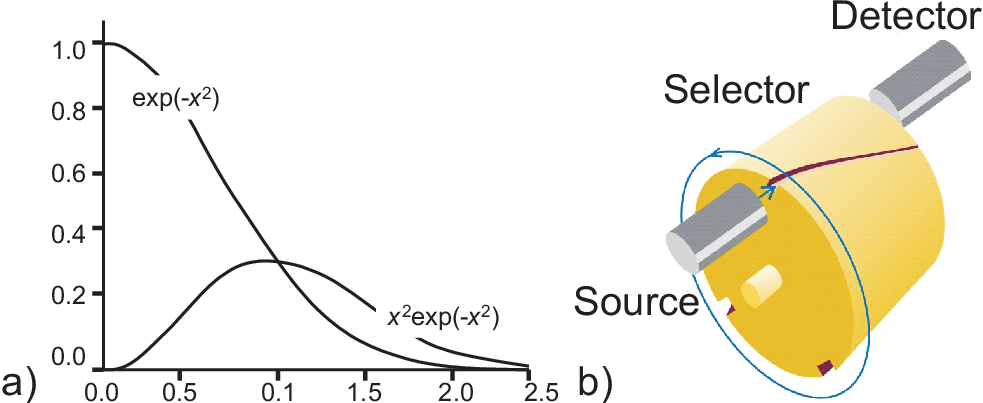
which is the famous Maxwell speed distribution. Fig. 4.1 a) shows the principle shape of this curve.
An experimental setup to measure explicitly the speed distribution of gasses is shown in Fig. 4.1 b): Particles at a specific temperature are produced in a source, e.g. an oven with a small hole in one wall. They travel in a beam towards the rotating channels. Only if the speed of a molecule is such as to carry it along the channel that rotates into its path it will reach the detector. Thus, the number of slow molecules can be counted by rotating the cylinder slowly, and the number of fast molecules counted by rotating the cylinder rapidly.
A second more implicit experimental approach is to determine the specific heat capacitance \(C_V\) as a function of temperature for a system which only shows translational kinetic energy contributions (no rotation, no oscillation), so

\begin{equation*} U = N_A m \overline{v^2} = \frac{3}{2} R T \quad \mbox{i.e.} \quad C_V = \frac{3}{2} R \quad . \end{equation*}

(4.19)

Figure 4.1: a) Principle curve of the Maxwell speed distribution. b) Selector setup to measure speed distributions.