3.3.2 Nucleation and Growth Modes

Nuclation in General

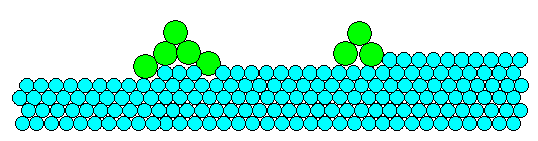
Let's suppose we have managed to get a few atoms "stuck", meaning physisorbed in polite terminology, on our substrate. At steps, or other defects, or whatever on our substrate A. We now ask two not-so-obvious questions:

Question 1: Are our nuclei -that's what we call those small primary agglomerates or clusters - stable and willing to grow?

Question 2: If they grow, what kind of general topology will the growing film assume?

Those may not have been the questions foremost in you mind, so let's first see why those are not only valid questions, but important questions. Let's look at question 1 first.

This is what we consider our starting point. We have a few small clusters of B-atoms physisorbed to the A-substrate. Will they grow if there are more B-atoms around that could be added to the pile?

Critical size of nuclei for layer growth

The answer, as always, is straight forward and simple: As long as we look at thermal equilibrium (or thereabouts), they will grow only if they free enthalpy of the total system decreases if the nuclei get bigger.

That should remind us of a quite similar problem we considered earlier in our study course: Will a three-dimensional defect, e.g. a precipitate with radius r, grow or not?

The problem was that the surface area and thus the surface energy always increases with r², while the decrease in the volume energy, which is the only reason why something should happen at all, goes with -r³. When we say energy, we mean, of course, always free enthalpy G.

The problem was that for small enough r the surface energy always "wins" and we found that growth is energetically only favored above a critical size expressed by r_crit and resulting from the interplay of volume and surface energy.

The situation in our case here as shown in the picture is exactly the same, just a bit more complicated. If you increase in your mind the size of one of the clusters, you will have done the following with respect to energy:

You decreased the energy of the A-surface because that surface gets smaller if you increase the cluster size (in all directions, of course).
You increased the energy of the A-B interface because its area gets bigger.
You increased the energy of the B surface because its area gets bigger.
You decreased the energy of the B-nuclei because its volume increases (and we assume that this lowers the energy of a bunch of B-atoms relative to them being "single").

If you think about this a bit, you will realize the essential curve for the free enthalpy will still look more or less like the red curve in the schematic drawing. If you want to look at the thinking already done, you activate the link.

The Wetting Angle and Its Significance

While the balancing of all those energies (and we could easily add more for more complex cases) in order to find the arrangement with minimum free enthalpy seems to be rather tricky, it turns out that you don't have to do it if you don't want details. It is sufficient to consider just on "simple" quantity, the wetting angle Q.

The name and the definition of the wetting angle comes, like many other names used in this context, from the early investigations of the (macroscopic) interaction of liquids and solids. You can't help noticing that a drop of water, if deposited on various substrates, forms spherical segments or culottes of various shapes; on greasy surfaces it is almost a sphere.

Solids that are deposited atom by atom on a substrate will behave quite similarly because you give them a choice of forming a shape for which surface and interface energies are minimized - and that's what the water drop does. If we assume that our material B deposited on substrate A actually assumes a shape that mimics to a large extent what a liquid would do, we end up with the following paradigmatical picture for the nucleation of thin films:

The surface or interface energies involved can be understood as forces pulling in the way indicated at the edge of the cluster of B atoms. For the wetting angle Q a simple relation follows:

g_SA	=	g_AB + g_SB · cos Q

cos Q	=	g_SA – g_AB g_SB

Now let's take it easy. What we obviously would like to have when we try to deposit a thin layer on a substrate is a wetting angle (also called contact angle) of Q=0^o so that the "drop" spreads out completely, producing a thin film.

This we can get if (g_SA – g_AB)/g_SB=1 or g_SA=g_SB + g_AB.

This is immediately clear. When we form the cluster as in the picture above, we reduce the total area of the substrate by some value A(r) given by the radius r (in fact, we have A(r)=pr²sin²Q). We thus take away the surface energy g_SAA(r) at the cost of having now some interface energy (g_ABA(r)) plus some surface energy of the B-material. If we "pay" no more in energy then what we get, the wetting angle will be zero because wetting the whole substrate cost nothing.

In fact, if we can cover the whole substrate area at a gain in energy, the film will also wet the substrate completely. A wetting angle isn't even defined anymore because its cosine would have values > 1.

The condition for getting smooth films, or the Frank - van der Merve layer-by layer growth mode, as we will call it from now on, is as follows:

g_SA	³	g_SB + g_AB

Now let's look at the other extreme; finite wetting angles (the maximum would be 180^o, meaning the cluster would be a little sphere just barely touching the substrate).

Obviously we simply need to have g_SA < g_SB + g_AB, meaning that we have to make the interface area smaller than the substrate area.

If g_SA is much smaller than the g_SB + g_AB, it just doesn't make energetic sense to cover the substrate; our thin film material B is better off just balling up.

The condition for getting rough or patchy films, or the Vollmer - Weber island growth mode, as we will call it from now on, is as follows:

g_SA	<	g_SB + g_AB

That would be it if the world would be simple. Luckily, it's not. We have something called Stranski-Krastanov layer-plus-island growth mode which looks like this

g_SA	>	g_SB + g_AB

plus strain

Details of that growth mode aren't all that clear. We need more than just the simple surface and interface energies of the perfect bulk materials A and B; strain that develops during the deposition, for example.

Look at the interface energy g_AB for a second. It will of course depend on the nature of A and B, but also on the exact structure of the interface. It might be epitaxial, for example and then possible strained so the lattices match. If that is so, there would be an increasing strain energy as the thickness increases.

In other words, the three surface and interface energies g considered are not absolute constants; they may depend on many things (surface reconstruction, for example), surface orientation, and so on.

	Some Generalization

	In total, what we have learned is that it is just not good enough to take some nice and clean substrate A and throw some atoms B at it (in some vacuum machine) if you want to produce a nice and smooth thin film. It may or may not work - there are many parameters to consider coming solely from properties of A and B - and we haven't even considered the many ways of "throwing atoms" yet!
	For the grand final let's look at the first moments of film growth again, the nucleation phase, and then at a later stage, well after nucleation.
		So we have a Frank - van der Merve layer-by-layer growth mode, let's say. Does that mean that the first thing we get is a complete layer, one atom thick, on our 300 mm Si wafer? You must be kidding, That takes a lot of atoms, and even if they perfectly "wet" the surface of the Si, the best you can expect is that a lot of small patches, one atom thick, will nucleate and than grow laterally by adding more incoming atoms at their edges. Finally, those flat islands of atoms coalesce and form a closed layer.
		Same story with the other growth modes. The Vollmer-Weber mode would lead to three-dimensional growth of lumps of atoms, that finally will coalesce into a closed, but bumpy layer.
		Of course, the "coalescence" might no be so easy and provide all kinds of defects, and of course, it just may happen that a second layer already nucleated and started growing laterally on top of a big patch before full coverage had been achieved.
	Anyway, sooner or later the substrate A will be completely covered by B - by a nice smooth layer, or by a rough sorry looking patchwork.
		How does it go on? We now deposit material B on material B and no longer on material A, after all.
		It depends. The Stranski-Krastonov layer-plus-island growth mode already demonstrated that there might be more than meets the eye. Nevertheless, things get a bit easier. There are only two surface and interface energies to consider, for example. In any case, you must expect that what is going to happen during the phase of growing B on B, is always more or less influenced by what happened at the nucleation phase.
	Last question: Where are the numbers? We put a lot of importance in surface and interface energies, so how about a few examples?
		Interestingly, neither the "Ohring" nor the "Smith" give (easily found) numbers. One simple reason for this is that there aren't any good numbers. Atomically clean surfaces do not exist under normal circumstances, making measurements difficult. (How would you measure a surface energy anyway?). Moreover, for crystals it also depends on {hkl}, the crystallographic orientation of the surface, and so on.