 |
We want to minimize the free enthalpy Gnuc of some nuclei - a cluster
of atoms (or molecules) of kind B on a substrate A. |
|
 |
One thing to do, just to make live easier, is to minimize the surface area of the cluster
of B atoms. We can do this by assuming that the cluster is a little sphere since the surface of a sphere has the
smallest surface per volume ratio. |
|
|
But that would defy the purpose so we just assume that the cluster can take any shape, and
if it can do that it would behave like a liquid. What we would get then is the shape of some liquid more or less "wetting " some substrate - water on glass or something like that. |
| |
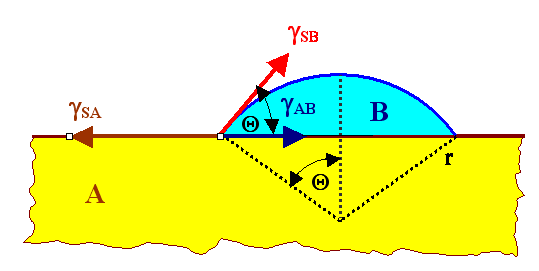
So we consider a situation like the one shown in the picture below: |
| |
|
|
Next we have to discuss a bit the meaning of the surface or interface energies
g. The basic definition is that it is simply the (differential) work dW
needed to increase the surface or interface area by dA. So we have |
| | |
|
| | |
|
In other words, the surface energy has the dimension of a stress or tension, and we may simply
interpret it as the force pulling back when you try to increase the surface in one dimension. |
|
|
This is symbolized by the arrows in the picture above. |
|
Obviously, in equilibrium, we need the forces to cancel and this gives us immediately a rather
important equation: |
| |
|
|
Obviously, if we know the three surface or interface energies involved, we can easily calculate
the contact angle or wetting angle
Q of the cluster. However, before we discuss this relation in more detail, let's first
write down the free enthalpy Gnuc of the situation. We have |
| |
| Gnuc |
= |
a3 · r3 · GV + |
a1 · r2 · gSB
+ |
a2· r2 · gAB
– | a
2 · r2 · gSA |
|
|
|
|
The meaning is clear. Gnuc is the energy (OK, free enthalpy change) of the
system containing a B-cluster with a size given by the radius r (without the cluster we put it at zero),
GV is the free enthalpy of the cluster, and the ai are the coefficients that
relate the volume of the cluster (the "cap"), the surface area of the cluster and the interface area to the radius
r (that describes completely the geometry of the arrangement). From (boring, but necessary) spherical geometry
we find: |
| |
| a1 |
= |
2p· (1 – cos Q) |
| | |
| | a2 |
= |
p · sin2 Q |
| | |
| | a3 |
= |
p/3 · (2 – 3cos Q + cos3
Q ) |
|
|
|
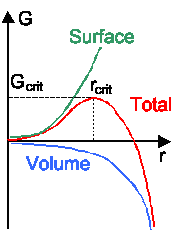
The first thing to note is that the equation for DGnuc
has cubic and quadratic terms in r and thus will give the general behavior shown in the backbone
and in the Introduction to Materials Science I. |
|
|
Thermal equilibrium is achieved if dGnuc/dr=0; and this will give us the
critical radius rcrit because it is just the radius at the minimum of G nuc(r)
and the critical free enthalpy Gcrit(rcrit) . Going through the differentiation
gives |
| |
| rcrit |
= | –2 · |
(a1 · g
SB+ a2· gAB– a2· gSA)
3a3 · GV |
| | |
| |
| |
| G crit |
= | 4 · |
16 p · (gSB)3)
3 · (GV)2 |
· |
2 – 3 cosQ + cos3Q
4 |
|
 |
|
|
|
Looking at the denominators of the equation above we see that we have a small critical radius
rV or a small Gcrit
if a lot of volume energy is gained, i.e. if GV is large, as it should be. |
|
|
Looking at the nominator, we see for rcrit the same kind of reckoning
up surface and interface energies as we had for the forces in the equation on top. Just
multiply with the respective areas expressed in the ai's, and you get energies. We have thus a
direct relation between the contact angle Q and the critical radius rcrit
or the critical free enthalpy Gcrit; the second equation for Gcrit already
expresses this fact. |
|
The contact angle Q is obviously a quantity
of major concern. It is a kind of direct account balance for the three competing interface energies, giving the energetically
best mix of interface areas for a given cluster size. |
|
|
Q can vary between Q=0o,
meaning that the cluster would spread into a thin layer, and Q=180o, meaning
that the cluster would form a perfect little ball touching the substrate just at one point. |
| |
The second term in the equation for G crit is only a
function of the wetting angle and looks like this (You can generate curves like that yourself in this
module). |
|
|
Note that for Q=0o (or 0p) the second fraction in the equation for Gcrit is zero, giving G
crit=0. For Q=180o, (or p) the
second fraction is =1 and Gcrit then increases with the third power of the surface energy
of the material to be deposited. |
| | |
|
|
Enough of basic nucleation theory a this point. We simply note two
major points:
- The formalism shown her is easily expanded to more complex situations (e.g. where stress and strain comes in) and, if
carried out, allows to obtain valuable information about what you must expect to happen when you try to deposit B
on A.
- A lot of relevant information can already be obtained by just considering the wetting angle Q
|
| | |
© H. Föll (Semiconductor Technology - Script)
4.2.1 Single Crystals Other Than Si 
With frame