|
Das einzige, was man über Solarzellen zunächst wissen muß, ist,
daß die "ideale" Solarzelle einfach eine flächige Diode, d. h. ein großflächiger pn-Übergang ist.
|
|
 |
Wir konzentrieren uns hier deshalb erstmal auf eine "ideale" Solarzelle
(die es in der harten Realität aber nicht wirklich gibt) und schauen uns deshalb als erstes den beleuchteten pn-Übergang an. |
|
 |
Wichtig ist dabei nur der Feldstrom. Schauen wir uns das
mal im Vergleich dunkel / beleuchtet an: |
|
|
 |
 |
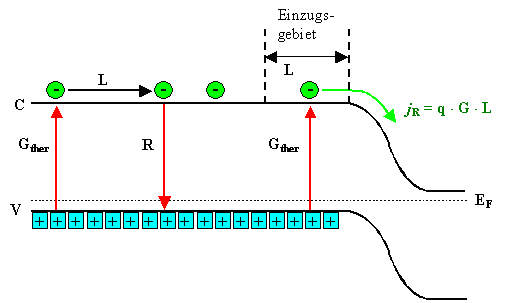
| Feldstrom im Dunkeln |
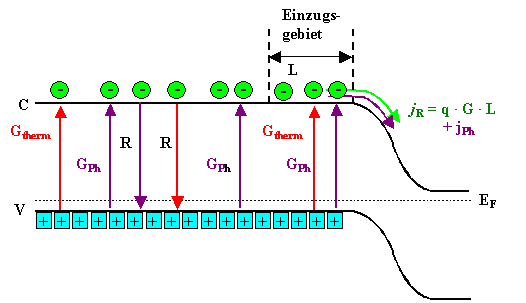
Feldstrom bei Beleuchtung |
|
| |
Hinweis: In dieser Abbildung sind die Teilströme noch englisch beschriftet:
Feldstrom = reverse current jR
|
|
 |
In Dunkeln ergibt sich der gezeigte Feldstrom der Elektronen
als Ladung q = –e mal rein thermische Generationsrate Gther
mal Einzugsgebiet = Diffusionslänge
L. Im Gleichgewicht rekombiniert weit weg von dem pn-Übergang genau so viel wie generiert wird,
d.h. die Rekombinationsrate R = G = nmin / t . |
 |
Jetzt beleuchten wir das Ganze mit Licht irgendeiner Intensität, das genügend
Energie hat, um die Bandlücke zu überwinden, d. h. hn
³ EG. |
|
 |
Überall im Halbleiter werden jetzt durch Absorption der Photonen zusätzliche
Elektron-Loch-Paare generiert, und zwar mit der zusätzlichen
Generationsrate GPh. Weit weg vom pn-Übergang verschwinden diese zusätzlichen
Ladungsträger wieder durch Rekombination. Die Rekombinationsrate geht dann ebenfalls entsprechend hoch und es gilt
weiterhin R = G, allerdings sind das nicht mehr die Gleichgewichtsraten! |
|
 |
In der Nähe des pn-Übergangs tragen die photogenerierten Minoritäten
jetzt aber mit jPh zum Feldstrom bei. Er erhöht sich damit auf |
| |
| jF(beleuchtet) | = |
jF(dunkel) + jF(Licht) |
|
|
|
 |
Wieviel Feldstrom jF(Licht) = j Ph produziert
wird, hängt in relativ klarer Weise offenbar im wesentlichen von Lichtintensität und Diffusionslänge ab. |
|
 |
Fertig . Wir haben alles,
was wir brauchen, wir müssen es nur noch aufschreiben oder aufmalen. |
 |
Wir gehen zurück zur Kennlinie des pn-Übergangs und verwenden
jetzt jF(beleuchtet) statt jF(dunkel) . Wir erhalten (was man auch direkt
sehen kann) für die Stromdichte-Spannungs-Kennline oder Diodengleichung
bei Beleuchtung: |
| |
| j (Uex) = |
æ
ç
è |
e · L · nMin (L)
t | + |
e · L · nMin(V)
t | ö
÷
ø
| · |
æ
ç
è |
exp ( | eU
ex
kBT |
) – 1 | ö
÷
ø
| – jF(Licht) |
|
|
 |
Wir müssen also von einer gegebenen Kennlinie immer nur jF(Licht)
oder, um einen anderen Namen zu benutzen, j F(solar) abziehen, denn alles andere bleibt unverändert.
Das gilt auch dann noch, wenn eine graphisch vorliegende Kennline auf sehr viel komplexeren Gleichungen als der obigen beruht.
Schauen wir uns die resultierende Kennlinie mal graphisch an. |
|
 |
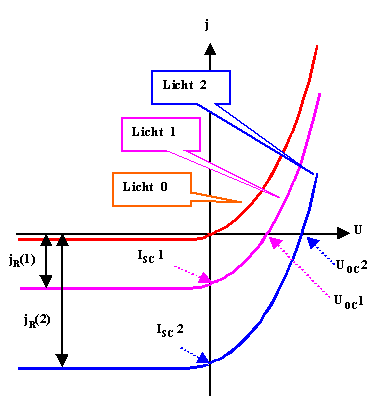
Wir schauen auf die alte Zeichnung
und ziehen – je nach Lichteinfall – einen mehr oder weniger großen konstanten (Feld-)Strom ab. Das sieht
dann so aus: |
| |
|
| |
Hinweis: In dieser Abbildung sind die Teilströme noch englisch beschriftet:
Feldstrom = reverse current j R
|
 |
Alles ist klar und berechenbar. Bei näherer Betrachtung sehen wir, daß
nur der 4. Quadrant interessant ist; er ist im rechten Bild groß dargestellt. |
|
 |
Offenbar erhalten wir bei Leerlauf (engl. "open circuit", abgekürzt OC), d. h. es fließt per definitionem
kein externer Strom, jetzt eine Leerlaufspannung UL
bzw. "open circuit voltage"
UOC an den beiden Enden des pn-Übergangs = Anschlüssen der Solarzelle. Sie ist
nach der obigen Formel berechenbar; das wollen wir auch mal in einer Übung tun. |
| |
|
|
 |
Als anderes Extrem könen wir die Solarzelle = pn-Übergang auch kurzschließen,
d. h. per definitionem ist die Spannung jetzt U = 0 V. Dann fließt der Kuzschlußstrom
IK bzw. der "short-circuit current" ISC,
der beträchtlich sein kann. Wie beträchtlich, sehen wir aus der schnellen Übung: |
| |
|
 |
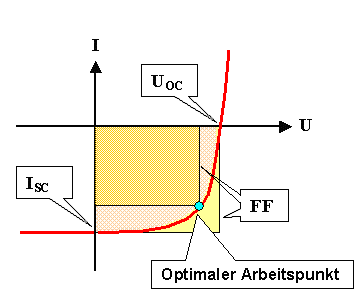
Wir wollen aber weder Strom I noch Spannung U, sondern
Leistung P = UI. Dazu definieren wir einen Arbeitspunkt
(d. h. einen Punkt auf der Kennlinie), bei dem UI maximal wird. Dieser optimale
Arbeitspunkt = Arbeitspunkt maximaler Leistung (engl.: maximum power point, MPP) definiert gleichzeitig den exakten
Wert des Verbraucherwiderstands. Auch dazu machen wir uns in der Übung
ein paar eigene Gedanken. |
 |
Im obigen Bild ist die Kennlinie zwischen zwei Rechtecken geführt, das kleinere
ist durch den optimalen Arbeitspunkt definiert. Die Fläche des großen Rechtecks ist offenbar UOC
· ISC, die Fläche des kleineren Rechtecks ist nicht auf Anhieb klar, aber bei gegebener
Kennlinie wohl berechenbar. Das Verhältnis der Flächen nennen wir den Füllfaktor (FF), er ist eine wichtige
Kenngröße von (realen) Solarzellen. |
|
 |
In Formeln: FF = UOC · ISC
/ (UMPP · IMPP) |
 |
Das sind einfache Definitionen, und wir halten mal fest: Leerlaufspannung, Kurzschlußstrom,
optimaler Arbeitspunkt, Füllfaktor, was immer wir wollen – wir können es über die Kennlinie ausrechnen, als Funktion der Material- und Technologie-Parameter
sowie der Temperatur . |
|
 |
Zum vollständigen Glück fehlt uns nur noch jF(solar) selbst,
der zusätzliche beleuchtungsbedingte Feldstrom. Der ist aber nicht so ganz einfach zu packen; wir geben uns damit zufrieden,
daß er groß wird, wenn die Diffusionslänge groß ist. |
| |
|
Maximaler Wirkungsgrad und absolute Energieproduktion |
| | |
 |
Was uns brennend interessiert, ist natürlich die bei allen Energiewandlern
immer im Vordergrund stehende Frage nach dem Wirkungsgrad
h, d. h. dem Verhältnis zwischen Energie raus und Energie rein (in %). |
|
 |
Wollen mal sehen. Die Sonne sendet uns Photonen mit allen möglichen
Energien – entsprechend allen möglichen "Farben" (die unsichtbaren inklusive), von Infrarot (IR
) bis zum Ultraviolett (UV).
Wir haben ein festes Sonnenspektrum. Es sieht (als Funktion der Wellenlänge l = c/n; n: Frequenz) so aus: |
| |
|
 |
Zunächst mal stellen wir fest: |
|
 |
Nur Photonen mit einer Energie größer als die der Bandlücke (oder l < hc/EG) werden im Halbleiter absorbiert. Sie befördern ein Elektron
aus dem Valenzband ins Leitungsband, generieren also ein Elektron-Loch-Paar und tragen damit zum Solarteil des Feldstroms
bei. |
|
 |
Für Si sind das im obigen Bild alle bei l < ca.
1 µm; wir nehmen also einen Teil der Infrarotstrahlung noch mit. Einen Teil aber verlieren wir, der Wirkungsgrad
h kann damit schon nicht mehr 100 % erreichen. Um diese Verluste zu vermeiden,
können wir natürlich einen Halbleiter mit kleinerer Bandlücke wählen, z. B. Ge. |
 |
Die Photonen mit genug Energie werden absorbiert und können damit brauchbare
elektrische Energie produzieren. Das tun sie aber nur mit Einschränkungen. |
|
 |
Den grundlegenden Prozeß der Absorption haben wir bereits betrachtet; hier ist nochmals
ein passendes Bild. Es zeigt, was ein Photon mit großer Energie im Si so anrichtet. |
| |
|
|
 |
Ein Elektron energetisch tief im Valenzband wird um hn >>
E G weit nach oben ins Leitungsband geworfen; ein hochenergetisches Elektron-Loch-Paar ist entstanden.
Die beiden frischgebackenen Ladungsträger werden sich aber sofort (innerhalb 10-13 s) auf energetisch
attaktivere Plätze begeben – die Löcher steigen auf zur Valenzbandkante, die Elektronen fallen runter auf
die Leitungsbandkante. Von der Anfangsenergie hn ist nur noch EG
übrig, der Rest hat nur das Si aufgewärmt. Das geht natürlich vom Wirkungsgrad ab. Was als nutzbarer
Anteil übrigbleibt, ist hier
gezeigt. |
|
 |
Die Lösung für diesen Verlust ist einfach: Wir nehmen einen Halbleiter mit größerer
Bandlücke, z. B. GaAs. |
 |
Wie nun – kleinere oder größere Bandlücke? Wir haben ein
klassisches Dilemma (griechisch; Zwangslage; Wahl zwischen zwei Übeln). Politiker
vermeiden in so einem Fall eine Entscheidung und fangen zur Ablenkung einen Krieg an (oder zerreden das Problem bis zur
Unkenntlichkeit); Theologen postulieren, dass durch göttliche Intervention irgendwie doch beides gleichzeitig geht
(z. B. Kinder haben und Jungfrau bleiben!). Ingenieure wissen, daß jetzt nur noch
die Optimierung hilft: Wir machen das Beste daraus. |
|
 |
Für terrestrische Anwendungen (als Abgrenzung zur
Raumfahrt) haben wir nur das solare Spektrum – so wie es bei uns auf dem Grund
des Luftozeans ankommt (oben eingezeichnet). |
 |
Damit erhält man folgendes Ergebnis (siehe hier): |
|
 |
1. Die optimale Bandlücke EGopt liegt bei
ca. 1,4 eV (also gerade noch im Infraroten); GaAs
würde als Material gut passen. |
|
 |
2. Der zugehörige maximale Wirkungsgrad ist hmax(E
Gopt) » 30 %. Mehr ist aus einer Solarzelle aus einem
Optimalmaterial nicht herauszuholen. |
|
 |
3. Für Si mit einem nicht optimalen
Bandgap von 1,1 eV erhält man hmax(Si) »
28 %. |
 |
Soweit zur idealen Solarzelle. Real erzielbare Wirkungsgrade mit realen (= billigen)
Solarzellen in einer Massenproduktion liegen deutlich niedriger. hreal(Si) » (15 - 17) % kann als derzeit (2009) guter Wert gelten. (Nachtrag: Im Jahr 2016 gilt
ein Wirkungsgrad um die 20 % als Standard.) |
|
| |
|
Die Sonne und Du |
| | |
 |
Was schickt uns die Sonnen an Lichtleistungs denn so? Am Äquator, in Kiel
oder sonstwo? Mittags oder um Mitternacht? |
|
 |
Wir merken uns nur Größenordnungen mit Zehnerzahlen. |
 |
Die absolute Leistungsdichte der Sonnenstrahlung (Äquator,
"high noon", keine Wolken) liegt ganz grob (und leicht zu merken) bei 1 kW/m2. Daran wird auch
noch so viel Forschung nichts ändern. Allenfalls die Zerstörung der Ozonschicht (O3) bringt
hier Fortschritte, wie ein Blick auf's Spektrum zeigt; aber zu Risiken und Nebenwirkungen
sollten Sie hier wirklich dringend ihren Arzt und Apotheker befragen (und eventuell Ihren Politiker schlagen)!
|
|
 |
Der maximale
Output einer Solarzelle mit h = 10 % liegt demnach – Faustregel – bei
100 W/m2. |
|
 |
Da aber auch am Äquator nachts die Sonne nicht scheint und in höheren
Breiten noch ein cos des Breitengrades einberechnet werden muß, wird man als Mittelwert über alles (Tag/Nacht,
Sonne/Regen, Sommer/Winter, Tropen/Arktik) ganz ganz grob allenfalls 10 % der Peakleistung im Jahresmittel ernten,
also gerade mal 10 W/m2. |
|
 |
Das sind aber alles glattte "Zehnerzahlen" zum Merken; in Wahrheit liegen
wir günstiger, derzeit (2009) in Deutschland etwa bei mittleren 13 W/m2 (weiterhin bezogen
auf den zuvor angesetzten Wirkungsgrad von 10 %) |
|
 |
Hier eine kleine Übersicht über wichtige "ungefähre"
Zahlen; im Zweifel immer pro m2. Der Link
bietet noch mehr Zahlen. |
| |
- Maximale Sonnenleistung: 1kW
- "Peak"-Leistung von Solarmodulen: 200 W
- effektiver Mittelwert Solarmodul übers Jahr: 25 W
- Mittlerer Solarenergieertrag pro Jahr: 25 W · 24 h · 365 = 219 kWh
- Jahresbedarf elektr. Energie pro deutschem Kopf: 1 750 kWh (wofür man die Stromrechnung zahlt)
- Platzbedarf (pro Kopf) für Solarzellen, um Elektrizität zu erzeugen: knapp 10 m2.
- Platzbedarf (pro Kopf) für Solarzellen, um alle Energie zu erzeugen: ca. 40 m2 .
|
|
 |
Dieser Link
führt zu einer Powerpoint-Präsentation zum Generalthema. |
|
| |
 |
Es kann also nur darum gehen, das prinzipiell Mögliche erst mal überhaupt
zu erreichen – und dann auch noch billig. |
|
 |
Wie wichtig das ist, wird anhand von Hintergrundinformationen zur Photovoltaik und zur allgemeinen Energiesituation deutlich (sehr empfehlenswert;
bitte diesen Link im Familien- und Freundeskreis verbreiten).
|
 |
Es wird Zeit für die Übungsaufgaben und die Verständnisfragen: |
| |
|
|
© H. Föll (MaWi für ET&IT - Script)