 |
Was geschieht am (idealen) pn-Kontakt, wenn wir, wie beim Volumen-Oberflächen-Kontakt,
jetzt eine externe Spannung anlegen? |
|
 |
Im Gegensatz zu dem bereits erfolgten Gedankenversuch in
dieser Richtung sollten wir das jetzt wirklich
tun. Dafür gibt es zwei Gründe: |
|
 |
1. Das geht! Ein Stück Si kann man
kontaktieren (wir übrigens auch bald). Sowohl zu p- als auch zu n-Si
können reale ohmsche Kontakte gemacht werden; es gibt weder technische noch begriffliche Schwierigkeiten.
|
|
 |
2. Wir erwarten, daß durch eine Diode Strom fließen
wird (und dann kein Gleichgewicht vorliegen wird), und dazu braucht man selbst
in einem Gedankenversuch einen geschlossenen Stromkreis mit Kontakten. |
 |
Unsere frühere Überlegung, was geschieht, wenn
ein externes Potential Uext angelegt wird, bleibt aber unverändert: |
|
 |
Wir müssen die linke und rechte Seite des Kontakts um eUext
gegeneinander verschieben. |
|
 |
Die Fermienergie ist dann aber nicht mehr konstant; im strengen Sinne gibt
es sie gar nicht mehr! Wir können also nicht mehr mit Schritt 1 des Gleichgewichtsrezepts
beginnen. |
 |
Andererseits wird weit weg vom pn-Übergang nicht viel passieren, was
vom Gleichgewichtszustand sehr verschieden ist. Falls jetzt Strom fließt, sind die Gebiete weit weg vom pn-Übergang
simple Leiter oder besser gesagt ohmsche Widerstände, und ihr Banddiagramm ist schlimmstenfalls leicht gekippt, wie
für diesen Fall bereits betrachtet. |
|
 |
Wir verlieren durch diese Bahnwiderstände
links und rechts vom pn-Übergang also allenfalls einen kleinen Teil der angelegten Spannung; dies werden
wir erstmal schlicht ignorieren. |
 |
Damit können wir links und rechts vom pn-Übergang
die Bandstruktur wie gewohnt zeichen, wir können sogar die Fermienergie wieder einzeichnen, um anzudeuten, daß
wir nicht weit weg vom Gleichgewicht sind. |
|
 |
Gegenüber der Gleichgewichtskonstruktion für Uext = 0
V müssen wir also nur eines der Bänder zusätzlich um eUext verschieben und
die beiden Bänder dann wieder "nach Gefühl" verbinden. Das sieht dann so aus: |
| |
|
|
 |
Falls wir rechts den Minuspol der Spannungsquelle
anschließen, erhöhen wir das Potential der Elektronen, die n-Seite rutscht um –eU
ext = +e|Uext| nach oben (oder die p-Seite nach unten; wir sind
frei bei der Wahl des Nullpunkts). | |
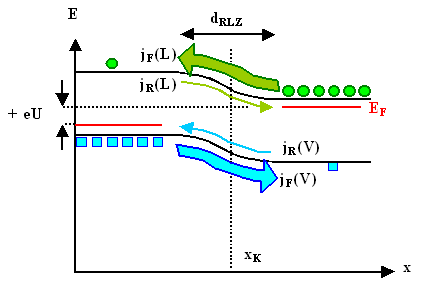
(Hinweis: In dieser Abbildung sind die Teilströme noch
englisch beschriftet: Diffusionsstrom=forward current jF, Feldstrom=reverse current jR) |
|
|
 |
Die Raumladungszone wird kleiner – "gefühlsmäßig", oder nach Formel –, falls wir statt D E
wieder DE
delta – eUext einsetzen (für diesen Fall ist
Uext also positiv). | |
|
 |
Die Energiebarriere wird kleiner. Der Diffusionsstrom
wird sich also deutlich erhöhen; es haben jetzt viel mehr Elektronen im n-Si und Löcher im p-Si
genügend Energie, um vom eigenen Schwung getragen über den Berg zu kommen. |
|
|
 |
Der Feldstrom
bleibt jedoch unverändert. Die Zahl der pro Sekunde an die RLZ-Kante kommenden Minoritäten ist
unverändert, und wie tief es hinuntergeht, spielt keine Rolle. |
|
| |
| |
|
|
 |
Das Potential der Elektronen (also die n-Seite) rutscht um eUext
nach unten (oder die p-Seite nach oben). | |
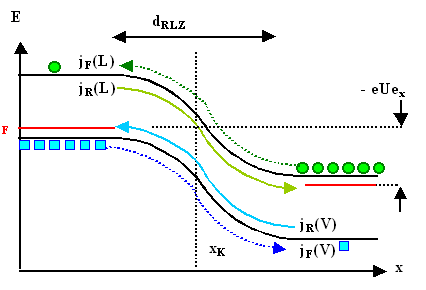
(Hinweis: In dieser Abbildung sind die Teilströme noch englisch
beschriftet: Diffusionsstrom=forward current jF, Feldstrom=reverse current jR) |
|
|
 |
Die Raumladungszone wird größer – "gefühlsmäßig",
oder nach Formel, falls wir statt DE F
wieder
DEF – eUext einsetzen (für
diesen Fall ist also Uext negativ). |
|
|
 |
Die Energiebarriere wird größer
. Der Diffusionsstrom wird also deutlich kleiner; wir können ihn vernachlässigen. |
|
|
 |
Der Feldstrom bleibt jedoch unverändert. Die Zahl
der pro Sekunde an die RLZ-Kante kommenden Minoritäten ist unverändert, und wie tief es hinuntergeht, spielt
keine Rolle. | |
|
 |
Als Nettostromfluß
jext(Uext < 0) im äußeren Stromkreis bleibt in Sperrichtung
also nur noch der Feldstrom. Er ist konstant und gegeben durch |
|
|
| jext (Uext < 0) |
= | æ
è |
jD(L) – |jF(L)| |
ö
ø | + |
æ
è |
jD(V) – |jF(V)| |
ö
ø |
» – |
æ
è | |j
F(L)| + |jF(V)| |
ö
ø |
|
|
 |
Nicht unflott! Wir haben ein typisches Diodenverhalten: Für eine Spannungspolarität
fließt ein mit der Spannung rasch zunehmender Durchlaßstrom
durch die Diode, für die andere Polarität ein konstanter spannungsunabhängiger Sperrstrom. |
|
 |
Durchlaßrichtung ist für n
egative Polung am n-Bereich, p
ositive Polung am p-Bereich – leicht zu merken. |
|
 |
Ob die Energie für eine gegeben Polarität rauf- oder runtergeht, ist ebenfalls leicht
zu merken: In Flußrichtung der Elektronen wird eine Energiebarriere niedriger, falls auf der anderen Seite ein positives
Potential dazukommt; für Löcher natürlich umgekehrt. |
 |
Alles, was uns noch fehlt, ist eine weitere Gleichung – wir müssen
die Spannungsabhängigkeit des Diffusionsstromes beschreiben. |
|
 |
Das können wir aber ziemlich einfach tun. Wir kennen zwei essentielle Eigenschaften des
Diffusionsstromes: |
|
 |
1. Er fließt über eine Energiebarriere (oder Energieschwelle)
der Gesamthöhe DEF ± e|Uext|.
Er fließt überhaupt, weil die stromführenden Teilchen eine durch die Temperatur bedingte Energieverteilung
haben und es einige damit schaffen können, die Energiebarriere zu überwinden. Damit muß er der allgemeinen
Formel für diesen Fall gehorchen, d. h. wir brauchen irgendeinen Vorfaktor c und den entsprechenden Boltzmannfaktor, der die von der externen Spannung Uext abhängige
Energiebarriere DEF – eUext enthält. |
|
 |
Damit ist schon alles klar – der Diffusionsstrom läßt sich wie folgt schreiben: |
| |
| jD (Uext) |
= c · exp ( – |
DEF – eUext
kBT | ) |
|
|
|
 |
2. Ohne äußere Spannung, d.h. im Gleichgewicht für Uext = 0,
ist der Diffusionsstrom in jedem Band für sich gleich dem (negativen) Feldstrom, d.h. jD(Uext=0) = –jF = |jF|.
Damit haben wir für jD(U ex): |
| |
| jD(Uext) = |
c · exp ( – | D
EF – eUext
kBT
| ) = |
c · exp ( – |
DEF
kB T |
) | · exp ( |
+ eUext
kBT |
) | | |
| | |
|| | |
| | | |
| |
jD(Uext=0)= |jF|
| | |
| jD( Uext ) | = |
|jF| · exp ( |
+ eUext
kBT |
) |
|
|
 |
Das war's. Wir müssen jetzt nur noch alles zusammensetzen und erhalten eine
erste Form der Diodengleichung (ab hier wird beim externen Strom j der Index
"ext" weggelassen): |
| |
| j(Uext) = |
æ
ç
è | |jF (L)|
| + | |jF(V)| |
ö
÷
ø | · |
æ
ç
è |
exp ( |
eUext
kBT |
) – 1 |
ö
÷
ø |
|
|
|
 |
Üblicherweise wird der Vorfaktor ( |jF(L)|
+ |jF(V)|) ganz simpel als j0 geschrieben –
denn man weiß ja, daß es der Betrag des Feldstroms ist. Außerdem kann, wie schon beim Stom, auch bei der
Spannung der Index "ex" weggelassen werden. Damit lautet die einfachste Form der Diodengleichung (was auch die
übliche Kennliniengleichung ist): |
|
|
| j (U) = | j0 |
· | æ
ç
è
| exp ( |
eU
kBT |
) – 1 |
ö
÷
ø |
|
|
|
 |
Aber Vorsicht: Das sieht einfacher aus, als es ist, denn wir müssen immer die Konvention
für die Vorzeichen der Ströme und Spannungen in der Diodengleichung berücksichtigen:
- Ströme in Durchlaßrichtung
werden immer als positiv betrachtet.
- Spannungen in Durchlaßrichtung werden immer als positiv
betrachtet.
Somit ergibt sich grundsätzlich ein Vorzeichenwechsel
zwichen der über der Diode extern angelegten Spannung Uext und der über dem pn-Kontakt
ohne Stromfluß intern abfallenden Spannung Ubi, mit der man z.B. die Weite der Raumladungszone
berechnet. |
|
 |
Zusätzlich wissen wir auch schon, wie groß die Sperrströme
sind: Generationsrate (= Rekombinationsrate = nMin(L) / t)
mal Einzugsgebiet (= L) mal Ladung (±e). Einsetzen ergibt die klassische
Diodengleichung: |
| |
| j(Uext) = |
æ
ç
è |
e · L · nMin(L)
t | + |
e · L · nMin (V)
t | ö
÷
ø
| · |
æ
ç
è |
exp ( |
eUext
kB T |
) – 1 |
ö
÷
ø |
|
|
|
 |
Schreiben wir die Minoritätsladungsträgerdichte mit Massenwirkungsgesetz
und Dotierung als
nMin = (ni) 2 / NDot, erhalten wir: |
| |
| j(Uext) = |
æ
ç
è |
e · L · (ni)2
NA · t | + |
e · L · (ni)2
ND · t |
ö
÷
ø | · |
æ
ç
è |
exp ( |
eUext
kB T |
) – 1 | ö
÷
ø
|
|
|
 |
Da die Diffusionslänge L und die Lebensdauer t
eng verwandt sind, kann man über die fundamentale Beziehung
L = (D · t )½ oder t = (L2
/ D) natürlich einen der beiden herauswerfen; man erhält dann zum Beispiel ... |
|
 |
... nach Eliminierung von t: |
| |
| j(Uext) = |
æ
ç
è |
e · D · (ni)2
NA · L | + |
e · D · (ni)2
ND · L | ö
÷
ø
| · |
æ
ç
è |
exp ( |
eUext
kB T |
) – 1 |
ö
÷
ø |
|
|
|
 |
... nach Eliminierung von L: |
| |
| j(Uext) = |
æ
ç
è |
e · (ni)2
NA |
æ
è | D
t | ö
ø
| ½ |
+ | e · (ni)2
ND | æ
è
| D
t |
ö
ø |
½ |
ö
÷
ø | · |
æ
ç
è |
exp ( |
eUext
kBT |
) – 1 |
ö
÷
ø |
|
|
 |
Und so weiter – man kann den Vorfaktor, der die Feldströme
enthält, in noch mehr Varianten schreiben – das kann man auch als intellektuelles Spiel sehen.
Die erste Version ist vielleicht am klarsten bezüglich der Natur der Ströme, die letzte bezüglich der entscheidenden Parameter.
|
|
 |
Schauen wir uns die wesentlichen Parameter noch einmal einzeln an:
- Der Diffusionskoeffizient
D der Ladungsträger ist primär eine Materialkonstante. Er ist über die Einstein-Beziehung
mit der Beweglichkeit
µ gekoppelt und damit etwas von Defekten, der Temperatur und der Dotierung abhängig.
- Die intrinsische Ladungsträgerkonzentration n
i ist eine echte Materialkonstante – sie spiegelt die Bandlücke wider – und natürlich
sehr stark die Temperatur.
- Die Diffusionslänge
L ist zunächst eine Funktion des Bandtyps (direkt oder indirekt) und dann ein Maß für die
Kristallperfektion.
- Die Dotierkonzentration
NDot ist der Technologieparameter – der einzig absichtliche!
Mit ihm können wir hier nicht furchtbar viel bewirken; aber das wird sich noch ändern.
- Die Temperatur
T steht explizit und implizit in der Formel. Einmal über ni, ein zweites Mal
über D bzw. µ, ein dritte Mal über NDot – bei tiefen
Temperaturen bricht die "mittlere Temperaturnäherung " zusammen! Auch wenn nicht jeder
Informatiker und Elektrotechniker es gerne hört: Realisierte Informations- und Kommunikationstechnologie ist angewandte
Thermodynamik (und selbstverständlich Quantentheorie).
- Die externe Spannung
Uext ist, wenn man so will, die Inputgröße, die Stromdichte j(Uext)
ist die Outputgröße der Diode.
|
|
| |
|
Eigenschaften der Kennlinie |
| | |
 |
Zunächst halten wir erstmal fest: Ein pn-Kontakt
ist immer eine Diode. Strom fließt
nur, falls die Polarität der angelegten Spannung "stimmt". |
|
 |
Das ist inzwischen fast eine Trivialität, aber wir haben inzwischen die
Ebene des Gedankenversuchs verlassen und sollten und darüber klar werden: Jeder von uns hat zu Hause so um die 100
000 000 - 10 000 000 000 pn-Übergänge um sich herum, die als unsichtbare (aber nicht immer wirklich stumme)
Diener für uns arbeiten. |
 |
Hätten wir nicht inzwischen eine intime Beziehung zur Kennlinienformel, könnte
man sie fast für furchteregend halten. Wir aber verstehen sofort die möglichen einfachen Näherungen: |
|
 |
Für
positive Spannungen am p-Si (leicht zu merken) ist
der Exponentialterm sehr schnell sehr viel größer als 1; wir können die "–1"
vergessen und erhalten für den Durchlaßstrom einer Diode in guter Näherung: |
| |
| jD » |
æ
ç
è |
|jF(L)| | + | |j
F(V)| | ö
÷
ø |
· | exp |
æ
ç
è |
eUext
kBT |
ö
÷
ø |
|
|
|
 |
In anderen Worten: Es handelt sich um eine simple Exponentialfunktion. Für eUext = kBT
(oder U
» 1/40 V) ist der Durchlaßstrom um einen Faktor e größer als
der Sperrstrom j F, d.h. immer noch ziemlich klein; aber für U
» 1 V ist er schon sehr viel größer (um e40!). |
 |
In Sperrichtung wird der Exponentionalterm schnell gegen null tendieren, d.h.
wir haben die extrem einfache Beziehung für den Sperrstrom (=Feldstrom): |
| |
|
|
 |
Einfacher geht's nicht. |
 |
Wie die Kennlinie jetzt aussieht, ist also hinreichend klar. Hier zwei Arten der
Darstellung: |
|
 |
Zuerst die einfache lineare
Auftragung. |
| |
|
|
 |
Hier die wesentlich aussagekräftigere Darstellung mit logarithmischer Stromdichte (und
Beträge von Spannung und Strom) |
|
|
|
 |
Zahlen sind absichtlich nicht eingefügt, denn die erarbeiten wir uns in Übungsaufgaben.
|
 |
So ganz langsam sollte jetzt eine ganz wichtige Frage hochkommen: |
|
 |
Stimmt das auch alles? Was
sagt das Experiment (denn nur das zählt!)? |
 |
Das Experiment sagt: Es kommt darauf
an – und zwar auf ziemlich viele Dinge. Zunächst haben wir den fundamentalen Unterschied: ideale Diode – reale Diode. Berechnet haben wir die
ideale Diode. Hier sind die Unterschiede: |
|
|
| Ideale Diode | Reale Diode |
| Geometrie |
"Unendlich" ausgedehnt ab Kontakt,
zumindest sind alle Abmessungen >> L |
Sehr klein; alle Abmessungen << L | | Dotierung | Konstant |
Variiert stark mit Entfernung vom Kontakt | | Bahnwiderstände | Keine |
Immer vorhanden | Parallelwiderstände
("lokale Kurzschlüsse") |
Keine | Je nachdem | | Einfluß Oberflächen | Keine |
Potentiell groß, da immer nahe zum Kontakt | | Zulässige Spannungen | Alle
|
Wird bei Durchlaßspannungen >> wenige V zu heiß; knallt durch bei zu hohen Sperrspannungen. |
| Generation/Rekombination in RLZ | Keine | Immer vorhanden |
|
 |
Alle Punkte bei der Realdiode mit Ausnahme des letzten
könnten wir eliminieren, falls wir uns Mühe geben und eine (technisch nutzlose) Diode bauen, die unserer Idealdiode nahe kommt.
|
|
 |
Was wir dann erhalten, läßt sich pauschal wie folgt ausdrücken
- Für Halbleiter mit relativ kleinen Bandlücken (< ca. 0,8 eV; z.B. Ge) stimmt die Theorie
ziemlich gut.
- Für Halbleiter mit relativ großen Bandlücken (> ca. 1 eV; z.B. Si) stimmt die Theorie
ziemlich schlecht. Insbesondere ist der tatsächliche Sperrstom viel zu hoch und leicht spannungsabhängig.
|
 |
Der wesentliche Grund ist, daß wir all die Ladungsträger, die in der
RLZ generiert werden (oder rekombinieren), einfach ignoriert haben. |
|
 |
Aber Generation findet auch in der RLZ ständig statt. Je nach Überschußenergie
und Impulsrichtung wird der irgendwo in der RLZ neugeborene Ladungsträger den Berg hinauflaufen oder hinunterfallen
– es werden also sowohl Durchlaß- als auch Sperrstromkomponenten in der RLZ erzeugt. |
|
 |
Das ist genau wie im richtigen Leben: Auch entlang des Abhangs gibt es Kneipen, die besoffene Radfahrer
generieren, die je nach Anfangsschwung und Richtung oben oder unten enden werden, und
Radfahrer, die "im Berg" vom Rad fallen, also in der RLZ
rekombinieren. |
 |
Die Berechnung dieser Stromkomponenten gilt i.a. als sehr schwierig; selbst im
Rahmen der schon selbst nicht übermäßig einfachen Shockley-Read-Hall-Theorie
ist einiger Rechenaufwand mit zahlreichen Annahmen und Näherungen notwendig. |
|
 |
Deswegen wollen wir hier nur zwei Anmerkungen machen: |
|
 |
1. Falls man die Raumladungszone in die Strombilanzen einbezieht, erhält man eine
Gleichung für die Kennlinie, die sehr gut stimmt – für alle Halbleiter. |
|
 |
2. Es ist aber gar nicht so schwer, die Teilströme aus der RLZ zu berücksichtigen.
Qualitativ ist es kein besonderes Problem, und mit ein bißchen intelligentem Raten erhält man sogar sofort die
richtigen Gleichungen. |
 |
Wir lassen das hier aber sein; die Neugierigen betätigen den Link. |
|
|
|
© H. Föll (MaWi für ET&IT - Script)