6.2.4 Der Beitrag der Raumladungszone zur Kennlinie des pn-Übergangs

Der Strombeitrag der Raumladungszone

	Was wissen wir über die in der Raumladungszone generierten Ströme?
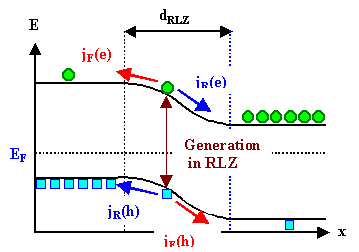
		Es wird an jeder Stelle eine Generationsrate geben, und die insgesamt pro Sekunde generierten Ladungsträger können als Ströme abfließen - zwei Teilströme im Leitungsband (Vorwärts und Rückwärts), und dasselbe nochmal im Valenzband. Schematisch sieht das so aus:
		Um ein Gefühl für die Größenordnung des Effekts zu bekommen, fragen wir uns zunächst: Falls alle Teilströme in eine Richtung fließen würden - wir groß wäre die Summe, der maximale Strom jmax(RLZ) der überhaupt aus der RLZ kommen könnte, im Gleichgewicht?
	Einfache Frage, einfache Antwort:
		jmax(RLZ) wird gegeben sein durch die Breite dRLZ multipliziert mit der Generationsrate GRLZ in der RLZ, denn das gibt uns die Zahl (immer pro cm2da wir Stromdichten betrachten) der pro Sekunde zur Verfügung stehenden Ladungsträger; wir haben
		jmax(RLZ)  =  2e · dRLZ · GRLZ
		Der Faktor 2 ist der erste (noch ziemlich bescheidene) Trick: Wir zählen beide Ladungsträger im Zweifel als Minoritäten, d.h. sowohl die Elektronen als auch die Löcher können Strombeiträge liefern. Wenn wir uns die Ladungsträgerdichten in der RLZ nochmals anschauen (Bild unten), sehen wir, daß das einerseits natürlich nicht stimmt, andererseits kann aber auch ein Majoritätsladungsträger in der RLZ zumindest zum Rückwärtsstrom beitragen, falls er energetisch "nach oben" läuft.
	Viel gravierender ist aber, daß die Generationsraten nach wie vor durch G = nmin/t gegeben ist.
		Da aber die Konzentration der Minoritätsladungsträger sich in der RLZ über viele Größenordnungen ändert und überdies sogar der Typ "umschlägt", haben wir jetzt ein massives Problem: Wir wollen die Gesamtzahl aller generierten Ladungsträger, und das involviert jetzt ein kompliziertes Integral, eine Aufsummation über die lokale Generationsrate G(x) - einerseits.
		Andererseits, was immer herauskommen würde - es läßt sich immer durch eine gemittelte Generationsrate GRLZ ausdrücken, die dann eine gemittelte Ladungsträgerdichte <nRLZ> braucht , d.h. <GRLZ> = <nRLZ> / t.
	Falls wir eine sinnvolle mittlere Dichte <nRLZ> erraten können, sind wir einen Schritt weiter. Was sollen wir nehmen?
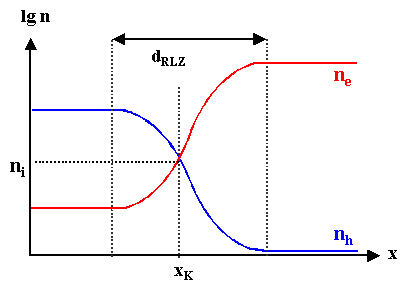
		Genau! Ein Blick auf die Ladungsdichteverteilung macht deutlich, daß sich ganz natürlich die intrinsische Ladunggsträgerdichte ni als Mittelwert anbietet; sie liegt notgedrungen zwischen den Extremwerten links und rechts; und was besseres können wir nicht erraten.
		Wir setzen also erstmal für den maximalen Strom aus der RLZ
		jmax(RLZ)  =  2e · dRLZ · ni t
	Das ist doch schon mal ein Anfang. Wir wissen aber noch mehr. Im Gleichgewicht fließt nach wie vor kein Nettostrom, und das bedeutet, daß sich der Strom aus der Raumladungszone genau hälftig auf die Vorwärts- und Rückwärtsrichtung aufteilen muß, wir haben
		| jF |(RLZ)  =  | j |R(RLZ)  =   jmax 2   =  e · dRLZ  ·   ni t
		Damit kennen wir bereits den Rückwärtstrom im Gleichgewicht, d.h. ohne äußere Spannung.
	Was passiert nun, wenn wir eine externe Spannung Uex anlegen und damit die Höhe der Energieschwelle ändern? Genau dasselbe wie bei der Betrachtung der Volumenbeiträge:
		Wie zuvor, nehmen wir einfach an, daß dem Rückwärtsstrom die Höhe der Energieschwelle ziemlich egal ist. Das ist zwar nicht ganz richtig, denn für große Sperrspannungen wird letzlich praktisch alles was in der RLZ generiert wird den Berg hinunterfließen, d.h. der Rückwärtsstrom wird gleich dem Maximalstrom aus der RLZ sein, und nicht nur die Hälfte davon - aber das macht gerade mal einen Faktor 2 aus. Im Rahmen unserer Trickserei können wir das großzügig ignorieren.
		Einen wesentlichen Unterschied zur Betrachtung der Rückwärtsströme aus dem Volumen gibt es aber schon: Die RLZ wird mit zunehmender Spannung größer - wir erwarten also, daß der Rückwärtsstrom aus der RLZ mit zunehmender Spannung zunimmt (mit der Wurzel aus Uex , um genau zu sein).
	Nun zur Vorwärtsrichtung. Die gesamte Energieschwelle ist wieder um – eUex kleiner als im Gleichgewicht für Uex = 0 V.
		Aber wir haben einen großen Unterschied zur Volumensituation: Je nachdem ob ein bestimmter Ladungsträger eher am Fuße oder eher am oberen Ende des Energiebergs generiert wurde, muß er fast den ganzen Energieberg überwinden, oder nur ein letztes kleines Reststück. In anderen Worten: Die Höhe der Energieschwelle für den Vorwärtsstrom ist - wie die Generationsrate - stark ortsabhängig.
		Wiederum müßten wir über die ortsabhängigen Boltzmannfaktoren aufsummieren, und wiederum verwenden wir denselben Trick: Wir nehmen einfach eine "mittlere" Energiebarriere, den Mittelwert aus maximaler Energieabsenkung (= eUex ) und minimaler Energieabsenkung (= 0 eV), also eUex /2.
	Damit können wir sofort den aus der RLZ stammenden Vorwärtsstrom hinschreiben:
		jRLZ, F(Uex)  =  jRLZ, R · exp –  eUex 2kT   =   e · ni · dRLZ t  · exp eUex 2kT
	Der gesamte Strom jRLZ(Uex) ist wie zuvor durch die Differenz  jRLZ, F  –  jRLZ, R  gegeben (mit einer Faktor 2 Unsicherheit), wir erhalten
		jRLZ(Uex)  =   e · ni · dRLZ t    · æ ç è exp eUex 2kT      – 1 ö ÷ ø
		Das ist - bis auf einen Faktor 2 - genau die Gleichung, die man bekommt, wenn man "richtig" rechnet.
	Damit erhalten wir die vollständige Diodengleichung in voller Schönheit (damit die Gleichung nicht zu lang wird verzichten wir auf die Indizes)
		j  =  æ ç è e · L · ni 2 t  · NA + e · L · ni 2 t  · ND ö ÷ ø  ·  æ ç è exp  eU kT  –  1 ö ÷ ø   +  e · ni · d(U) t  æ ç è exp eU 2kT  –  1 ö ÷ ø
		Die Größen L und t beziehen sich auf die jeweiligen Teilchensorten (im ersten Summand die Elektronen, im zweiten die Löcher), denn sie können im Prinzip für Löcher und Elektronen verschieden sein.

	Das ist jetzt eine nicht mehr auf den ersten Blick zu überschauende Gleichung; wir müssen sie diskutieren. Zuerst betrachten wir die Vorwärtsrichtung.
		Sobald wir die "–1" vernachlässigen können, ergibt sich der Vorwärtsstrom in halblogarithmischer Auftragung als die Überlagerung zweier Geraden mit relativer Steigung 1 und ½. Für kleine Spannungen gewinnt dabei immer die kleine Steigung; dies ist im folgenden Diagramm leicht zu sehen.
		Für kleine Spannungen und damit auch Ströme "gewinnt" der Vorwärtsanteil der Raumladungszone.
		Was dabei "klein" heißt, hängt von der Diffusionslänge bzw. Lebensdauer ab. Kleine Diffusionslängen, d.h. schlechte kristalline Qualität, führt zur Ausdehnung der "Steigung ½" Zone
		Auch der Einfluß der Temperatur ist für den Volumen- und RLZ Anteil verschieden. Aber das ist alles Stoff für Übungsaufgaben.
		Insgesamt erwarten wir eine (logarithmische) Kennlinie mit einem "Buckel" in Vorwärtsrichtung. Die Größe des Buckels ist ein indirektes Maß für die kristalline Qualität des Materials.
		Der Faktor 2 im Nenner war mehr oder weniger geraten. In der Realität kann er andere Werte haben. Oft nennt man den gemessen Zahlenwert den Idealitätsfaktor n der Diode. "Ideale" Dioden hätten dann n = 1.

	Wie sieht es in Rückwärtsrichtung aus? Dazu bilden wir einfach das Verhältnis aus den Rückwärtsströmen des Volumens (jR(Vol)) und der Raumladungszone (jR(RLZ)), und bekommen
		jR(Vol) jR(RLZ)  =  e · (ni)2 · L t · NDot e · ni · dRLZ t  =  ni · L NDot · dRLZ
	Der entscheidende Faktor ist ni/NDot.
		Mit zunehmender Energielücke nimmt ni exponentiell ab; der Volumenanteil des Rückwärtsstroms wird bei "großen" Bandlücken gegenüber dem Raumladungszonenanteil zu vernachlässigen sein.
		Mit zunehmender Temperatur nimmt ni exponentiell zu (während NDot, die Konzentration der ionisierten Dotieratome ziemlich konstant bleibt). Damit wird bei hohen Temperaturen wieder das Volumen dominieren.
	Damit können wir jetzt einen Blick auf gemessene Kennlinien werfen:
	Das sieht doch schon ganz gut aus:
		Beim Ge spielt der Einfluß der Raumladungszone keine große Rolle (d.h. ni >> NDot); die gemessene Kennlinie würde der gezeigten theoretischen Kennlinie ganz gut folgen.
		Beim Si, mit einer Energielücke bei der sich offenbar der Anteil der Raumladungszone deutlich bemerkbar macht, ist der "Buckel in Vorwärtsrichtung klar zu erkennen; in Rückwärtsrichtung ist der Sperrstrom weit größer als die simple Theorie vorhersagt und leicht spannungsabhängig - paßt!
	Daß noch einige zusätzliche Effekte dazukommen - bei zu hoher Spannung in Rückwärtsrichtung wird es irgendwann knallen, ohmsche Widerstände (= Bahnwiderstände) werden sich bei hohen Strömen bemerkbar machen, etc. - wen wundert's. Aber das soll uns hier nicht weiter beschäftigen.
		Wir haben damit ein ziemlich umfassendes Verständnis des pn-Übergangs erreicht - ohne ein einziges Mal richtig gerechnet zu haben.
		Fragebogen / Questionaire Multiple Choice Fragen zu 6.2.4

© H. Föll (MaWi 2 Skript)