6.2.5 Zusammenfassung Kapitel 6.2

Der pn-Übergang

	Das Banddiagramm des pn-Übergangs erhält man nach "Rezept":
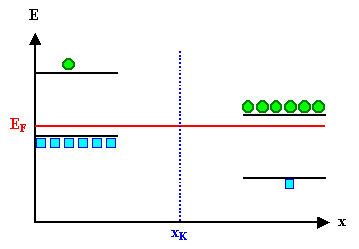
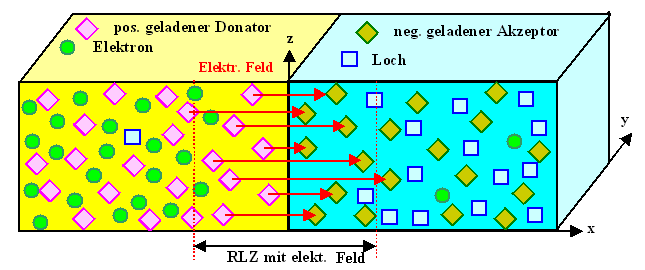
	In der mit der Bandverbiegung immer verbundenen Raumladungszone (RLZ) sitzen die ortsfesten ionisierten Dotieratome.
		Die beweglichen Elektronen und Löcher fehlen in der Raumladungszone - falls einer dieser Ladungsträger sich dorthin verirrt, wird er sofort durch das elektrische Feld "hinausgeworfen".
		Die damit verbundenen Ströme müssen im Mittel = 0 sein, dies ist im rechten Diagramm angedeutet.
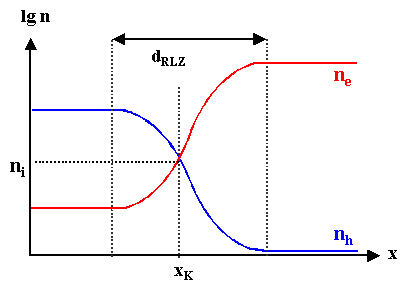
	Im Ortsbild sieht ein pn-Übergang und die Konzentration der beweglichen Ladungsträger wie folgt aus:
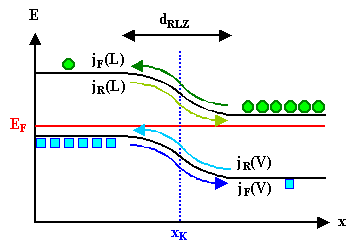
	Die über den pn-Übergang fliessenden Ströme kann man für Löcher und Elektronen getrennt betrachten. Für jede Ladungsträgerart gibt es immer zwei gegenläufige Komponenten:
		Majoritätsladungsträger fließen energetisch "aufwärts"; diese Stromkomponente heißt Diffusionsstrom, Rekombinationsstrom oder Vorwärtsstrom jF. Nur wenigen der vielen Majoritäten wird es gelingen, die Energiehürde zu überwinden und zu diesem Strom beizutragen.
		Minoritätsladungsträger fließen energetisch "abwärts", diese Stromkomponente heißt Feldstrom, Driftstrom, Generationsstrom oder Rückwärtsstrom jR. Alle der wenigen Majoritäten, die an die Kante der RLZ gelangen, werden den Energieberg "hinunterfallen".
		Im Gleichgewicht müssen beide Ströme gleich groß sein; jF = – jR.
	Für den Rückwärtsstrom kann man sofort eine Formel angeben. Er muß proportional sein zum Einzugsgebiet der RLZ und damit zur Diffusionlänge L (nur Minoritäten, die während ihres "random walk" überhaupt bis zur RLZ kommen, können "hinunterfallen") und zur Generationsrate G = nR/t (es kann nicht mehr abfließen als was nachgeliefert wird).
		Im Gleichgewicht (keine äußere Spannung und damit kein Nettostrom) haben wir unter Verwendung des Massenwirkungsgesetzes, der Annahme, daß alle Dotieratome ionisiert sind und des "übergeordneten" Wissens, dass die Proportionalitätskonstante = 1 ist
		jR(L)   =  – jF(L)   =  – e · L · nMin(L) t    =  – e · L · (ni)2 NA · t jR(V)   =  – jF(V)   =  – e · L · nMin(V) t  = – e · L · (ni)2 ND · t
	Mit einer externen Spannung Uex wird die Energiehürde größer oder kleiner - je nach Vorzeichen.
		Das hat aber nur Auswirkungen auf den Vorwärtsstrom - seine Größe relativ zum Gleichgewichtsfall ändert sich mit einem entsprechenden Boltzmannfaktor; wir haben
		jF(Uex)   =  jF(Uex = 0)  =  – jR · exp eUex kT
	Die (vorzeichenrichtige) Addition aller 4 Teilströme unter Berücksichtigung der Vorzeichenkonvention Ströme in Durchlaßrichtung werden immer als positiv betrachtet Spannungen in Durchlaßrichtung werden immer als positiv betrachtet ergibt die (elementare) Diodengleichung
		j(Uex)  =   æ ç è e · L ·nMin(L) t + e · L ·nMin(V) t ö ÷ ø · æ ç è exp eUex kT   –  1 ö ÷ ø
		Diese Gleichung läßt sich in vielen Varianten schreiben, je nachdem welche Parameter man bervorzugt (L und t wie oben, oder D und t, oder .... .
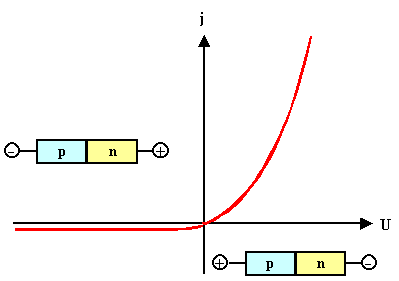
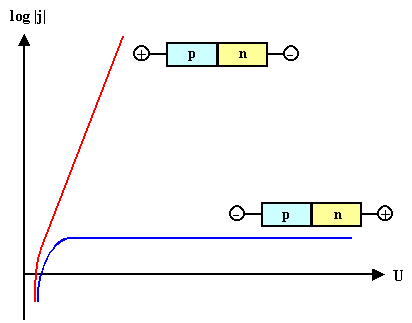
	Graphisch sieht das in linearer oder (besser) halblogarithmischer Auftragung so aus:
	In der Formel stecken jedoch viele Idealisierungen, die bei realen Dioden zu kurz greifen.
		Insbesondere werden auch in der RLZ Ladungsträger generiert (oder rekombiniert). Das läßt sich nur mit erheblichem Aufwand (und vielen Näherungen) halbwegs sauber quantitativ fassen; jedoch gibt auch schon eine simple Plausibilitätsbetrachtung die richtige Formel für den Diodenstrom unter Berücksichtigung der RLZ Komponenten:
		j  =  æ ç è e · L · ni 2 t  · NA + e · L · ni 2 t  · ND ö ÷ ø  ·  æ ç è exp  eU kT  –  1 ö ÷ ø   +  e · ni · dRLZ(U) t  æ ç è exp eU 2kT  –  1 ö ÷ ø
	Für das Verhältnis der Rückwärtsströme nur aus dem Volumen und nur aus der RLZ folgt
		jR(Vol) jR(RLZ)  =  e · (ni)2 · L t · NDot e · ni · dRLZ t  =  ni · L NDot · dRLZ
	Damit wird für alle Halbleiter mit "großer" Bandlücke oder ni << NDot der Rückwärtsstrom (= Leckstrom) durch den RLZ Anteil dominiert. Damit ist der RLZ Anteil zum Diodenstrom technisch sehr wichtig.
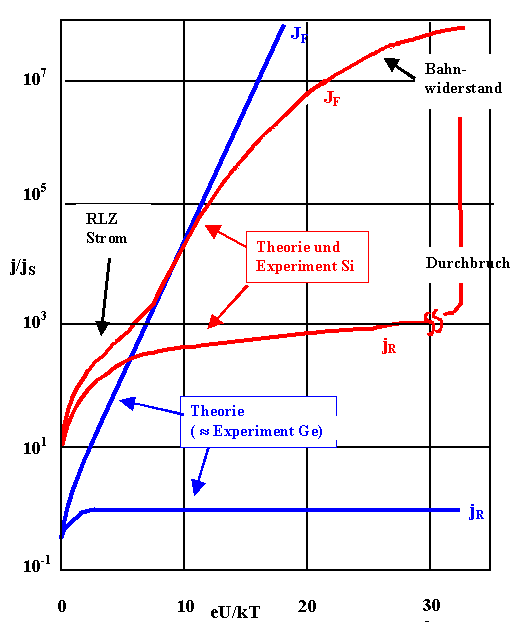
		Insbesondere ist Si in diesem Zusammenhang ein Halbleiter mit großer Bandlücke, dies zeigt sich in dem (immer noch stark idealisiertem) Vergleich der Theorie und des Experiments

© H. Föll (MaWi 2 Skript)