9.2.2 Darstellung der Stromleitung im Banddiagramm

	Im Banddiagramm läßt sich die Stromleitung, d.h. der Transport elektrischer Ladungen von hier nach da, sehr gut und einleuchtend darstellen.
		Um elektrische Ströme zu erhalten, brauchen wir ein elektrisches Feld E, bzw eine Spannung U, bzw. eine Potentialdifferenz DV zwischen hier und da. Falls wir "da" erden, ist DV = U.
		Wir ersparen uns hier den üblichen Krampf mit den limitierten Buchstaben und benutzen den Buchstaben E auch für das elektrische Feld - aber dann in Magenta!
	Bleiben wir eindimensional wie auch sonst, haben wir nun ein Stück Halbleiter mit verschiedenem elektrischem Potential bei x = 0 und x = L.
		Im Banddiagramm betrachten wir die Energie der Elektronen im Kristall. Was bedeutet es, wenn jetzt ein elektrisches Potential V(x) vorliegt?
		Ganz einfach: Wir müssen zu der aus den Bindungen im Kristall kommenden Energie E, die wir bisher ausschließlich betrachtet haben, noch die elektrostatische Energie – e · V(x) addieren, und erhalten jetzt eine ortsabhängige Energie E(x).
		Denn das elektrische Potential mal der betrachteten Ladung gibt ja gerade die potentielle Energie dieser Ladung in dem zu V gehörenden elektrischem Feld an.
	Den Zusammenhang zwischen Ladungen r(x,y,z), elektrischem Potential V(x,y,z) und elektrischem Feld E(x,y,z) gibt dabei immer die Poisson-Gleichung
		DV =  ¶2 V ¶x2   +  ¶2V ¶y2  +  ¶2V ¶ z2  =  – Ñ · E =  – r   ee0
	Aber das müssen wir hier gar nicht so genau wissen. Wir betrachten einfach ein Stück Halbleiter, an dessem einen Ende (x = 0) das elektrische Potential den Wert V(0) = –V0 hat, während das andere Ende (x = L) geerdet ist, d.h. V(L) = 0. Die Maßeinheit ist natürlich Volt.
		Was jetzt kommt ist wichtig. Also nochmal: Wir betrachten ein homogenes Stück Material – z. B. einen zylindrischen Draht – mit irgendeiner Leitfähigkeit s und damit einem Widerstand R. An einem Ende ist er geerdet (d. h. die Spannung ist 0 V per Definition), an anderen Ende liegt die Spannung U Volt an. Außerdem fließt noch ein Strom I = U/R.
		Spannung anlegen bedeutet: An einem Ende (z. B. dem negative Pol) hat es mehr negative Ladungen als am anderen Ende. Im System gibt es räumliche Nettoladung.
		Zwischen den beiden Enden fällt die Spannung ab. Das kann sie bei der beschriebenen Anordnung nur gleichmäßig tun – sie fällt linear von einem Ende zum andern von U V auf 0 V.
		Betrachten wir nicht die Spannung oder das "Spannungspotential" U sondern die elektrostatische Energie eU, die eben auch Potential heißt, haben wir exakt denselben Verauf, nur auf einer eV Skala statt auf einer V Skala.
	Das wenden wir jetzt auf ein homogenes Stück Halbleiter mit konstantem Querschnitt an.
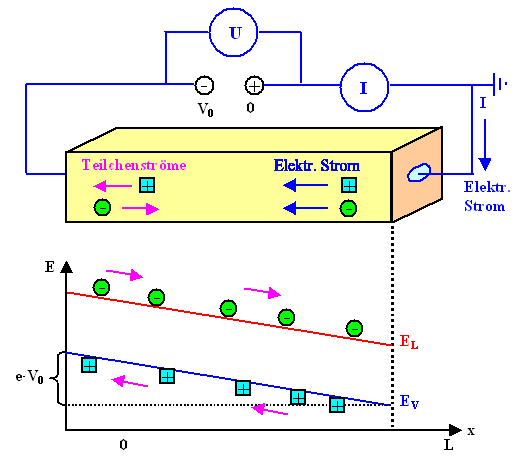
		Es ergibt sich das folgende Banddiagramm, das wir erst mal zur Kenntnis nehmen, und dann diskutieren.
	Das Bild zeigt eine Fülle von Einzelheiten, die wir jetzt im Detail diskutieren:
		Im oberen Teil ist perspektivisch das Material gezeigt – mit den elektrischen Kontakten und dem Stromkreis. Man sollte niemals ein Banddiagramm und eine Darstellung im Ortsraum verwechseln – auch wenn auf einer hohen Abstraktionsebene beides nur noch ein Rechteck ist.
		Eingezeichnet ist ebenfalls, wie sich negativ und positiv geladene Teilchen bewegen werden. Wichtig dabei ist, daß trotz unterschiedlicher Teilchenstromrichtung, beide Ladungen dieselbe elektrische Stromrichtung ergeben.
		Weiterhin ist klar, daß bei konstanter Leitfähigkeit der Spannungsabfall im Material linear erfolgt. Dies bedeutet, daß das lokale elektrische Potential eV(x) linear von eV0 eVauf  0 eV abnimmt.
	Damit kann man das Banddiagramm zeichnen:
		Links sind Valenz- und Leitungsband auf der Energieskala um |– e · V0| angehoben; rechts ist alles beim alten. Dazwischen nimmt die Energieanhebung linear ab - wie gezeichnet. Aufpassen! Das "-" Vorzeichen ist richtig, wenn man die Energieachse nach unten legt (Nullpunkt oben, Energiewerte dann alle negativ)
		Das ist leicht zu verstehen, denn nach wie vor betrachten wir im Banddiagramm die gesamte Energie von Elektronen in den beiden Bändern (Im Valenzband in Form von Löchern). Die Gesamtenergie erhält man immer durch Addition der Beiträge, hier der "Kristallenergie", d. h. der Energie, die die Elektronen auf ihren Zuständen im Kristall haben, und der Energie des lokal vorliegenden elektrostatischen Potentials.
	Wir haben damit eine fundamentale Sache eingeführt, die sogenannte Bandverbiegung. So nennen wir es, wenn Leitungs- und Valenzband nicht exakt horizontal verlaufen.
		Gleichzeitig erkennen wir eine fundamental Regel:
		Bandverbiegungen sind immer mit elektrischen Feldern im Material gekoppelt.
		Denn ein elektrisches Feld ist schlicht der Gradient des elektrischen Potentials, und ohne Gradient im Potential gibt es keine Bandverbiegung.
	Rein graphisch wird schon anschaulich was nun geschieht: Die Elektronen im Leitungsband werden sich zur tiefsten Energie begeben - sie laufen in einem Energiediagramm immer bergab. Da sie beweglich sind, wird das auch geschehen.
		Die Elektronen im Valenzband werden sich auch zur tiefsten Energie begeben. Da aber nur ein kleiner Teil beweglich ist – die mit einem Loch als Nachbar – laufen die Löcher entgegengesetzt, immer den Energieberg hinauf. Das ist eingezeichnet.
		Falls viele Elektronen "unten" wären, gäbe es unten einen Überschuß an negativer Ladung, oder, im Umkehrschluß, es gäbe oben einen Überschuß an positiver Ladung. Zeichnen wir nicht den Fluß der negativen Ladung nach unten ein, müssen wir den Löchern jetzt eine positive (Elementar)ladung nach oben mitgeben. Das ist eingezeichnet.
	Wir sehen also auch im Banddiagramm, daß jetzt Ladungen fließen. Wir sehen es sogar viel anschaulicher als im Ortsraum. Wo aber liegt nun die Fermienergie? Sie ist nicht eingezeichnet !?
		Das hat einen einfachen, aber sehr wichtigen Grund: Es gibt im strengen Sinn keine Fermienergie mehr – denn wir haben nicht mehr Gleichgewicht. Mit Stromfluß haben wir Ungleichgewicht!
		Denn Stromfluß bedeutet immer Ungleichgewicht oder Nicht-Gleichgewicht. Es gibt zeitliche Änderungen von Systemparametern: Der Halbleiter wird warm, in der Batterie ändert sich die chemische Zusammensetzung, usw.
		Die Fermienergie war aber nur für Gleichgewicht definiert; sie existiert nicht für Nicht-Gleichgewicht.
	Das fassen wir mal zusammen
		Bandverbiegung bedeutet: Leitungs- und Valenzband sind keine horizontale Linien mehr, sondern "verbogen". Grund: Zusätzliches elektrisches Potential. Damit gilt: Verbiegung = Anwesenheit elektrisches Feld E. Elektronen und Löcher spüren im Feld E die Kaft qE. Damit: Elektronen laufen in nicht-horizontal Bändern abwärts, Löcher aufwärts. Falls dann Nettostrom fließt, ist der Halbleiter nicht mehr im Gleichgewicht. Kein Gleichgewicht bedeutet: Fermieenergie ist nicht mehr (streng) definiert. Gründe für Bandverbiegungen sind Nettoladungen irgendwo im System.
	Ein letzter Punkt: Das Banddiagramm zeigt nicht, was mit den Elektronen und Löchern geschieht, wenn sie bei ihrer Berg- und Talfahrt an das Ende des Kristall gelangen.
		Wir wissen aber, was geschehen muß: Die Spannungsquelle ist eine Ladungspumpe, sie befördert die Elektronen, die bei x = L ankommen, durch den äußeren Stromkreis wieder zurück nach x = 0.
		Löcher allerdings kann die Spannungsquelle nicht durch einen Metalldraht pumpen. Sie wird deshalb bei x = 0 Elektronen ins Valenzband geben, die mit den Löchern rekombinieren, und bei x = L diese Elektronen herausnehmen, d.h. Löcher injizieren. Das mag hier noch ein bißchen seltsam erscheinen, wir werden diese Prozesse aber bald besser verstehen.
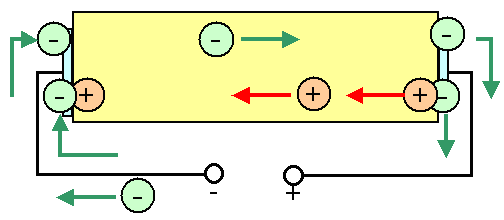
		Die Zeichnung zeigt die Ströme im Halbleiter und im Draht; die Pfeile geben dabei die Bewegungsrichtung der Teilchen an, nicht die technische Stromrichtung. Für Löcher sind beide Richtungen identisch, für Elektronen sind sie umgegekehrt.
	Wir haben jetzt einen ersten Eindruck bekommen, wie man mit Banddiagrammen arbeiten kann. Wer testen möchte, inwieweit er das verstanden hat, versuche mal, sich die folgende Frage zu beantworten, bevor die Lösung angeklickt wird:
		Was passiert im Banddiagramm, wenn wir wie oben eine Spannung anlegen, aber die Kontaktelektroden mit einer "unendlich dünnen" isolierenden Schicht überziehen?
		Das bedeutet, wir haben zwar den Potentialunterschied zwischen x = 0 und x = L, aber Stromfluß kann dank der Isolierschicht nicht stattfinden.
	Die Antwort auf diese Frage findet sich in einem eigenen Modul, den man unbedingt konsultieren sollte.
		Fragebogen Schnelle Fragen zu 9.2.2

© H. Föll (MaWi für ET&IT - Script)