|
Die Leitfähigkeit s = Si
qi · ni · m
i umfaßt die jetzt bekannten Ladungsträgerkonzentrationen n
und deren Beweglichkeit m |
|
| D | = | µ · kBT
e |
| Einstein
Beziehung | | |
| | | | µ |
= | D · e
kBT |
|
|
|
|
 |
Die in ihren Bändern beweglichen Elektronen und Löcher diffundieren
, d. h. führen einen "ramdom walk" aus, mit einer Diffusionskonstante
D | |
|
 |
Diffusionskonstante und Beweglichkeit beschreiben beide "random walk", müssen
also korreliert sein. Die Beziehung zwischen beiden heißt "Einstein (-Smoluchowski)
Beziehung". | |
| | |
| |
 |
Beweglichkeiten sind an Stöße gekoppelt. Wichtige Stoßpartner
waren "Phononen" (=thermische Gitterschwingungen) und Kristalldefekte. | |
|
|
 |
Dotieratome sind Defekte. Sie verringern damit die Beweglichkeit (und damit die Leitfähigkeit
ein bißchen) aber erhöhen die Ladungsträgerdichte (und damit die Leitfähigkeit enorm) |
|
|
 |
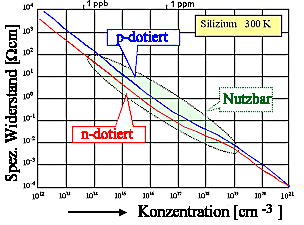
Der Gesamteffekt der Dotierung von Si bei RT ist in der Masterkuve gezeigt:
Þ | |
|
 |
Die "Beulen" im ansonsten ziemlich linearen Verlauf kommen von der Änderung
der Beweglichkeit mit NDot; die Unterschiede zwischen n- und p-Dotierung stammen
von verschiedenen Beweglichkeiten der Löcher und Elektronen. | |
| | |
| | |
 |
Legt man eine Spannung U an einen Halbleiter, addiert (oder, je
nach Vorzeichen, subtrahiert) man die Energie eU. | |
|
|
 |
Die Bandkanten rutschen entsprechend rauf oder runter. | |
|
 |
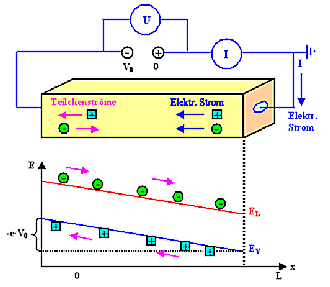
Fällt die Spannung gleichmäßig über den Halbeiter ab, erhält man
eine Bandverbiegung wie gezeigt. Þ | |
|
 |
Entscheidende Punkte sind:
- Leitungs- und Valenzband sind "verbogen".
- Grund: Zusätzliches elektrisches Potential.
- Verkippung = elektrisches Feld E.
- Elektronen laufen abwärts, Löcher aufwärts.
- Falls Nettostrom, kein Gleichgewicht mehr.
- Gründe für Bandverbiegungen sind: Nettoladungen irgendwo im System.
| |
| |
| | |
|
© H. Föll (MaWi für ET&IT - Script)