Bandverbiegung im "Kondensator"

	Wenn wir einen Halbleiter zwischen zwei isolierte Elektroden bringen, machen wir eine Art "Kondensatorversuch", der Halbleiter ist dann das "Dielektrikum".
		Es ist sehr illustrativ, sich erst mal zu überlegen, was im Material geschieht, wenn wir gedanklich nacheinander einen Isolator, einen Leiter = Metall und einen Halbleiter zwischen die Platten unseres Kondensators stecken.
		Es ist noch illustrativer, sich dabei qualitativ den Verlauf der Ladungsgsdichte, des elektrischen Feldes and des Potentials zu überlegen.
		Obwohl das für ein Metall oder einen Isolator eigentlich zum Basiswissen gehört, ist der Fall des Halbleiters als Dielektrikum neu. Im Link wird die Thematik im Detaisl behandelt.
	Wie auch immer: Klar ist, daß bewegliche Ladungen zur Kondensatorplatte mit der entgegengesetzten Ladung laufen: Elektronen zu positiven; Löcher zur negativen Seite.
		Das wird so lange geschehen, bis alle Ladungen auf der Kondensatorplatte einen "Partner" im Halbleiter haben. Wir erwarten also an der positiven Platte eine Anreicherung an Elektronen, und an der negativen Platte eine Abreicherung (was gleichbedeutend ist mit einer Anreicherung an Löchern).
		Wir erwarten auch, daß nach einer kurzen Umverteilungsphase Gleichgewicht herrscht.
	Mehr muß man nicht wissen, um ein qualitatives Banddiagramm konstruieren zu können. Da wir hier zum ersten Mal ein Grundrezept zur Konstruktion von Banddiagrammen aller Arten durchkochen, machen wir es in 2 Schritten.
		Wir starten mit zwei harten Fakten: Da wir Gleichgewicht haben, ist die Fermienergie per definition überall gleich. Wir können sie also als horizontale Linie zeichnen. Tief im Inneren des Halbleiters wird man von den geladenen Kondensatorplatten an den beiden Enden nichts mehr merken. Dort muß die Fermienergie deshalb in Bandmitte liegen.
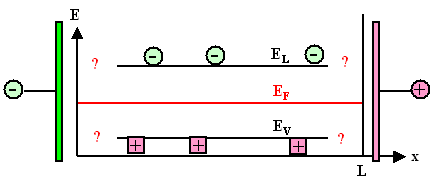
		Damit können wir Teile des Banddiagramms zeichnen:
		Die Fermienergie ist überall dieselbe; die Gleichgewichtskonzentration von Elektronen und Löchern im Inneren des Materials ist angedeutet. Im Grunde fehlt nur noch die geladenen Randschicht. Wie sieht sie aus im Banddiagramm?
	Das ist eigentlich ganz einfach: Wir wissen, daß am rechten Rand die Elektronenkonzentration erhöht sein muß. Das kann sich nur auf Elektronen im Leitungsband beziehen, andere können nicht nach rechts wandern. Wir wissen auch, daß die erhöhte Konzentration zeitlich stationär ist, da wir Gleichgewicht haben.
		Damit ist die lokale Konzentration der Elektronen und Löcher (nL(x) bzw. n V(x)) in jedem Abstand von der Elektrode durch die immer gleiche Generalformel gegeben:
		nL (x)  =   NLeff · exp – EL(x)  –  EF kT      nV(x )  =  NVeff · exp – EF   –  EV(x) kT
	Die Konzentrationen sind jetzt ortsabhängig, und damit muß die Energie von Leitungsbandkante und Valenzbandkante ebenfalls ortabhängig werden - es gibt sonst keine Möglichkeiten mehr, Ortsabhängigkeiten einzubringen.
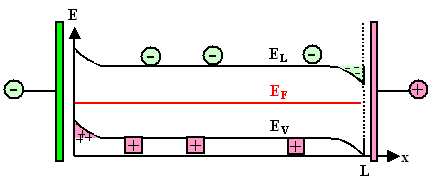
		Eine Erhöhung der Elektronenkonzentration erfordert eine Erniedrigung von EL(x) – EF ; für die Löcher muß EF – EV(x) kleiner werden. Damit kann man das Banddiagramm fertigstellen:
		So "ungefähr" muß das Banddiagramm aussehen. Was wir allerdings hier nicht wissen können, ist die Ausdehnung der Bandverbiegung - in E- und x- Richtung.
		In anderen Worten: Wir wissen weder, wie tief die mit Elektronen oder Löcheren angereicherte Zone ins Innere des Materials eindringt, noch wie groß die Verbiegung auf der Energieachse ist. Aber das werden wir bald ändern.
	Wir wissen aber schon, daß in Bereichen verbogener Bänder immer ein elektrisches Feld vorliegt. Die Ausdehnung der Bandverbiegung entspricht deshalb der Eindringtiefe des von den Kondensatorplatten ausgehenden elektrischen Felds.
		Dieser Eindringtiefe eines elektrischen Feldes in das Innere eines Materials geben wir einen Namen; sie heißt Debye-Länge.
		Die Debye-Länge eines gebenen Materials ist ein ziemlich fundamentaler Materialparameter; wir werden ihr (im Hauptstudium) noch oft begegnen. Nicht nur bei Halbleitern, sonder auch z.B. bei Ionenleitern.
	Es ist wichtig sich klar zu machen, daß dieses Rezept zur Konstruktion von (qualitativen) Banddiagrammen im Gleichgewicht immer funktioniert! Wir werden es noch oft benötigen.

Mit Frame

9.2.2 Darstellung der Stromleitung im Banddiagramm

8.3.4 Leitfaehigkeit intrinsischer Halbleiter

© H. Föll (MaWi für ET&IT - Script)