8.3.3 Effektive Zustandsdichte und Boltzmann-Näherung

	Die Grundformeln für die Ladungsträgerdichte
	Wie groß ist die Dichte nL der Elektronen im Leitungsband eines Halbleiter mit jetzt gegebener Zustandsdichte?
		Einfach: Die Antwort auf eine Frage dieser Art ist immer dieselbe: (Volumen)dichte der Plätze (N(E) = D(E) · DE) mal Wahrscheinlichkeit, daß ein Elektron draufsitzt (Fermiverteilung; f(E; EF, T) und dann aufsummieren (= integrieren). In Formeln also
		nL =  ¥ ó õ EL D(E) · f(E; EF, T) · dE
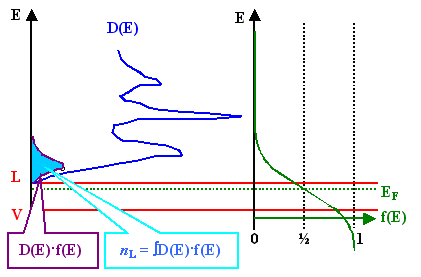
		Für Puristen: Wir dürfen bis ¥ integrieren, da die Fermiverteilung bei großen Energien sowieso alles auf null setzt. Das sieht man ganz gut in dem folgenden Bildchen:
		Für alle: Man tut gut daran, sich die Zeit zu nehmen, um dieses Bildchen gut zu durchdenken und wirklich gut zu verstehen – und zwar bezüglich seiner Aussage, wie nLrechnerisch zustandekommt.
	Wir machen uns das Leben einfach und benutzen zwei Näherungen: Die Boltzmann-Näherung f(E; EF, T) » exp[–(E – EF)/(kBT)]. Das ist eine gute Näherung, solange die Fermienergie einige kBT unter der betrachteten Energie E liegt. Die Näherung der effektiven Zustandsdichte. Das ist eine gute Näherung, solange die Fermienergie einige kBT unter der betrachteten Energie E liegt – s.o. Wir ersetzen das Integral dann durch die simple Formel: nL  »  Neff · exp[–(EL– EF)/(kBT)]
		Für die 2. Näherung benutzen wir schlicht die Tatsache, daß ein bestimmtes Integral letztlich eine Zahl ist, und die kann man unter den gegebenen Umständen auch wie gezeigt schreiben. Damit müssen wir jetzt als neuen (und einfacheren) Materialparameter die effektiven Zustandsdichten Neff für die verschiedenen Halbleiter bestimmen – getrennt für Leitungs- und Valenzband; statt einer Kurve nur noch eine Zahl.
		Das tun wir durch Nachschauen in der Literatur. Hier sind die wichtigsten effektiven Zustandsdichten; für Si auch noch mit der (immer vorhandenen) Temperaturabhängigkeit:
		Halbleiter   Effektive Zustandsdichte (in 1018 cm–3) Leitungsband Valenzband Silizium (Si) 24 15 Germanium (Ge) 10 6 Galliumarsenid (GaAs) 0,5 7 Galliumnitrid (GaN) 0,5 3 T / K 100 200 300 500 1000 Silizium: Neff(T) (in 1018 cm–3) 4,59 13,0 23,9 51,3 145
		Wir nehmen zur Kenntnis, daß die effektiven Zustandsdichten im Leitungs- und Valenzband etwas verschieden sind, werden aber, um die Dinge einfach zu halten, diese Unterschiede in Zukunft ignorieren.
		Wir nehmen auch noch gerade so zur Kenntnis, daß man, je nachdem, wo man nachschaut, etwas verschiedene Zahlen findet. Ab und zu wird die Zustandsdichte auch noch mal mit verbesserten Methoden nachgemessen; wenn man es genau wissen will, kommt man also nicht darum herum, erst mal die neueste wissenschaftliche Literatur zu konsultieren.
	Wir beschließen diesen Abschnitt mit den drei Grundformeln, die wir noch sehr oft brauchen werden:
		Dichte neL der mit Elektronen besetzten Plätze im Leitungsband               neL  =  Neff · exp( – EL – EF kBT  )             Dichte nhV der Löcher, also der nicht besetzten Plätze im Valenzband               nhV  =  Neff · exp( – EF – EV kBT  )             Massenwirkungsgesetz               neL ·  nhV  =  Neff2 · exp( – EL – EV kBT  ) = const.(T) = ni2(T)                             ni(T): intrinsische Ladungsträgerdichte
	Bei einem intrinsischen Halbleiter liegt im thermodynamischen Gleichgewicht die intrinsische Ladungsträgerdichte vor, und zwar sowohl im Leitungs- wie im Valenzband: nhV = ni = neL
	Das gibt uns Gelegentheit für eine schöne Übungsaufgabe:
		Übungsaufgabe 8.3-2 Massenwirkungsgesetz
		Außerdem haben wir natürlich noch die schnellen Fragen:
		Fragebogen Schnelle Fragen zu 8.3.3

© H. Föll (MaWi für ET&IT - Script)