|
Energieerhaltung beim Band-Band-Übergang |
| |
 |
Wir betrachten jetzt nur noch Halbleiter. Sie unterscheiden
sich von Isolatoren zunächst nur durch die Möglichkeit, daß die bei
Raumtemperatur verfügbare thermische Energie (kBT)RT
» 1/40 eV ausreicht, um einigen wenigen Elektronen den Sprung vom (vollen) Valenzband
ins (leere) Leitungsband zu ermöglichen. |
|
 |
Der Übergang von Elektronen vom Valenzband ins Leitungsband sowie der umgekehrte
Prozeß, der Übergang von Elektronen im Leitungsband zu freien Plätzen im Valenzband, sogenannte Band-Band-Übergänge, sind also unmittelbar verantwortlich für die elektrische
Leitfähigkeit der Halbleiter. Wir müssen sie etwas näher betrachten. |
|  |
Jeder solcher Übergang bedeutet einen Wechsel von einem Zustand mit einem
Wellenvektor k1 zu einem neuen Zustand mit einem Wellenvektor k2.
Dabei ändern sich Energie und Impuls
des Elektrons. |
|
 |
Da aber der Energie- und der Impulserhaltungssatz auch in der Quantentheorie
gelten, müssen wir uns mit den damit verbunden Konsequenzen beschäftigen. |
 |
Wir betrachten zunächst den Energieerhaltungssatz.
Der Klarheit halber nehmen wir Photonen, also Licht, mit der eindeutig definierten Energie
EPhoton = h · n
, um Elektronen aus dem Valenz- ins Leitungsband zu lupfen. |
|
 |
Das Photon trifft ein Elektron irgend"wo" im Valenzband
unseres Halbleiters. Das "wo" bezieht sich dabei sowohl auf den Ort im Ortsraum als auch im k-Raum.
In der folgenden Zeichnung hat das "getroffene" Elektron den Zustand k; damit ist alles über
den Zustand "vorher" gesagt: |
|
|
|
|
 |
Für den Zustand "danach" gibt es nun zwei Möglichkeiten:
1.) Die Energie des Photons reicht aus, um das Elektron mindestens bis zur Unterkante des nächsthöheren
Bandes zu heben.
2.) Die Energie des Photons reicht dafür nichtaus. |
|
 |
Eine weitere Möglichkeit gibt es nicht, da das untere Band das Valenzband und also komplett
gefüllt ist; freie Plätze stehen nur im oberen Band (dem Leitungsband) zur Verfügung. |
 |
Zur ersten Möglichkeit: Falls die Photonenenergie groß genug
ist, um das Elektron mindestens bis zur Unterkante des nächsthöheren Bandes zu heben, wird das mit einer gewissen
Wahrscheinlichkeit auch passieren. |
|
 |
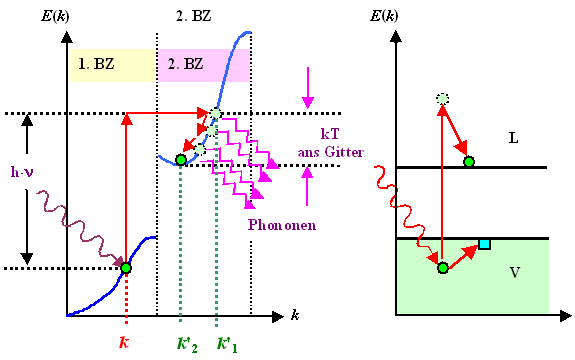
Im obigen E(k)-Diagramm gibt es aber bei der Energie hn über dem Start-Zustand k
gar keinen Zustand; wir müssen das Elektron also in den energetisch passenden Zustand in der 2.
BZ "transferieren" (roter Pfeil nach rechts). Dadurch hat das Elektron dann einen anderen (größeren) Wellenvektor.
|
|
 |
Das Elektron "sitzt" also nun im Zustand k'1
im sonst leeren Leitungsband. Da es nun für unser Elektron jede Menge freie Plätze bei kleineren Energien
gibt, wird es nicht lange auf seinem ersten Platz bleiben, sondern sich von Platz zu Platz "nach unten" sinken
lassen, bis es das Energieminimum des Leitungsbandes bei
k'2 erreicht hat; angedeutet durch die kleinen roten Pfeile nach unten. |
|
 |
Die Überschußenergie geht dabei portionsweise ins Gitter, d. h. der
Kristall wird ein bißchen wärmer. In der Zeichnung ist das formal-abstrakt so dargestellt, daß das hinunterhüpfende
Elektron Phononen emittiert. (Phononen sind die Teilchen, die quantisierten Gitterschwingungen entsprechen –
analog zu den Photonen als Lichtteilchen.) |
|
 |
Dieser Prozeß heißt Thermalisierung. Er erfolgt sehr schnell –
in 10–13 bis 10–11 Sekunden ist alles vorbei. |
 |
Zur zweiten Möglichkeit: Falls die Photonenenergie nicht groß
genug ist, um das Elektron mindestens bis zur Unterkante des nächsthöheren Bandes zu heben, passiert nichts!
Und das ist eine sehr wichtige Aussage! |
|
 |
Denn das bedeutet, daß es für hn
< EG
keine Absorption des Photons geben kann. Für Photonen mit kleinerer Energie als
die der Bandlücke ist der (perfekte) Kristall komplett durchsichtig ! |
|  |
Es sind also auch fundamentale optische Eigenschaften im Banddiagramm enthalten! |
 |
Die Darstellung im Banddiagramm rechts ist natürlich wieder viel einfacher,
weil wir uns nicht um die k-Werte kümmern. Dafür können wir hier eine andere wichtige
Sache einfacher wiedergeben als im E(k)-Diagramm: Das ins Leitungsband transferierte Elektron
hinterläßt einen unbesetzten Platz im Valenzband, ein "Loch"; es ist als kleines blaues Quadrat eingezeichnet. |
|  |
Das Loch ist der einzige freie Platz, auf den das Elektron aus dem Leitungsband zurück
ins Valenzband springen könnte. Weil aber auf diesen freien Platz sehr leicht auch die anderen Elektronen im Valenzband
springen können, die energetisch höher sitzen als das Loch, rückt das Loch ziemlich fix an die Oberkante
des Valenzbandes. |
|
 |
Das geschieht sehr schnell – denn auch hier geht es um Thermalisierung. Weiter unten
(und in den folgenden Abschnitten) mehr zu den Löchern, jetzt wir müssen uns erst noch um folgendes Thema kümmern:
|
|
Impulserhaltung beim Band-Band-Übergang |
| |
 |
Wir müssen nun den Impuls des Systems
vorher und nachher
betrachten. Das ist erheblich schwieriger als die Betrachtung der Energie, da der quantenmechanische Impuls von Photon,
Kristall und Elektron nicht so unmittelbar klar ist wie die Energie. |
|
 |
Wir müssen hier etwas an der Oberfläche bleiben und werden einige "Dinge"
einfach postulieren. Trotzdem läßt sich eine wichtige Beziehung leicht verständlich
machen: |
|
 |
In der Quantenmechanik ist der Impuls immer
gegeben durch |
| |
| Impuls | =
p = 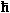 · k · k |
|
|
|
 |
Das gilt für Elektronen, Photonen und Phononen. Da die Wellenlängen von (Licht-)Photonen
immer sehr viel gößer sind als die der Elektronen und Phononen (l
von Photonen liegt im Bereich von 1 µm, bei Elektronen und den hier wichtigen Phononen eher im nm-Bereich),
ist ihr Wellenvektor entsprechend viel kleiner. Damit können wir den Impuls der Photonen in
1. Näherung schlicht komplett vernachlässigen . |
|
 |
Zum Merken: |
|
|
Photonen haben Energie, aber
kaum Impuls.
Phononen haben Impuls, aber kaum Energie.
Elektronen haben Impuls und
Energie. |
|
|
 |
Es geht damit nur noch um den Impuls des Elektrons "vorher" (im Valenzband;
Wellenvektor k) und "nachher" (im Leitungsband; Wellenvektor k').
|
|
 |
Für den Unterschied schreiben wir Dp,
die Differenz des Impulses nachher minus dem vorher. Wir haben: |
|
|
| Dp = |
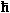 · (k' – k) · (k' – k) |
|
|
|
 |
Diese Differenz ist auf jeden Fall nicht null, und das ist ein Problem, denn der Impulserhaltungssatz
sagt, daß diese Impulsdifferenz exakt ausgeglichen werden muß – und das bedeutet, daß der Impulserhaltungssatz
für das Elektron ohne
dritten Partner (der sich um diese Impulsdifferenz kümmert) nicht zu erfüllen
ist. |
 |
Das Besondere an dieser Situation ist zudem, daß im perfekten Kristall auch
der Impulserhaltungssatz von der Perfektheit des Kristalls beeinflußt ist; ohne weitere Herleitung nehmen wir zur
Kenntnis, daß der Impulserhaltungssatz im Kristall lautet: |
| |
k' – k = G
G = reziproker Gittervektor |
|
|
 |
Das sollte uns nun sehr bekannt vorkommen. Es ist die gute alte Bragg-Bedingung
– mit einer Verallgemeinerung: |
|
|
| |k| = |k'|
braucht nicht mehr erfüllt zu sein! |
|
|
 |
Das bedeutet, daß wir jetzt auch inelastische
Streuung zulassen – und also bildet das Kristallgitter als Ganzes den erforderlichen dritten Partner, ohne
den der Impulserhaltungssatz für das Elektron nicht zu erfüllen wäre. Deshalb spricht man hier auch vom Kristallimpulserhaltungssatz. |
|
 |
Ob das nun einfach oder kompliziert ist, sei dahingestellt, es hat jedenfalls einschneidende Konsequenzen! |
|
| |
|
Reduziertes Banddiagramm
|
| |
 |
Wenn wir die Darstellung des Band-Band-Übergangs im E(k)-Diagramm
oben wieder betrachten, bedeutet Impulserhaltung nun, daß der nach rechts weisende
rote Pfeil entweder die Länge null oder die Länge eines reziproken Gittervektors
haben muß. |
|
 |
Das hat er aber sicher nicht, denn in der Zeichnung wäre der kürzestmögliche
reziproke Gittervektor so lang wie beide Brillouinzonen zusammen – man erinnere sich, daß die Ränder der
Brillouinzonen bei der Hälfte der reziproken Gittervektoren liegen! |
|
 |
Die Konsequenz ist einfach: Der oben gezeichnete Band-Band-Übergang
kann gar nicht stattfinden, denn er verletzt den Kristallimpulserhaltungssatz! |
|
 |
Um Energie- und
Kristallimpulserhaltung gleichzeitig zu erfüllen, müßten wir also im E(k)-
Diagramm solange mit zwei vorgegebenen Strecken (den beiden roten Pfeilen) an der Dispersionskurve
rauf- und runterfahren, bis wir zwei k-Werte finden, bei denen alles paßt. Das tun wir aber nicht,
sondern wir lassen uns etwas einfallen, das die Arbeit sehr stark erleichtert. |
 |
Die E(k)-Diagramme lassen sich sehr viel platzsparender
zeichnen, wenn man eine kleine Vereinbarung bezüglich eines zeichentechnischen "Tricks" trifft: Wir malen
alle Zweige der E(k)-Kurven der diversen Brillouin-Zonen in die 1. Brillouin-Zone. Man
weiß ja, zu welcher BZ irgendein Ast gehört – man muß nur von unten kommend abzählen. |
|
 |
Praktisch geht das ganz einfach: Wir verschieben jeden Ast solange um reziproke
Gittervektoren nach innen, bis er in die 1. BZ fällt. Das sieht so aus: |
| |
|
|
 |
Diese "Sparversion" der E(k)-Kurven heißt
reduzierte Darstellung oder reduziertes
Banddiagramm. (Es ist die allgemein übliche Form des Banddiagramms, daher läßt man das "reduziert"
in der Praxis wieder weg.) |
 |
Damit sparen wir nicht nur eine Menge Platz, sondern die von Impuls- und Energieerhaltungssatz
erlaubten Übergänge liegen jetzt einfach senkrecht übereinander. (Zur
Erinnerung: Das liegt daran, daß ein Photon praktisch keinen Impuls hat und sich also bei einem solchen Übergang
der Kristallimpuls nicht ändert.) |
|
|
|
|
 |
Das ist leicht einzusehen: Jeder Übergang, der energetisch paßt, erfüllt
automatisch den Kristallimpulserhaltungssatz, denn die diversen Äste der E(k)-Kurve unterscheiden
sich ja genau durch einen reziproken Gittervektor. |
|
 |
Die Absorption eines Photons sieht jetzt also so aus wie links dargestellt. Die Länge
des Pfeils mit der Energie hn muß nur noch an die passende Stelle zwischen den zwei
Ästen gezeichnet werden. |
 |
Wir wollen diese Vereinbarung, für Band-Band-Übergänge das reduzierte
Bandschema zu verwenden, zukünftig automatisch einhalten. (Dies ist im übrigen auch durch die harte Theorie zu
rechtfertigen, die unter der Bezeichnung "Bloch-Theorem" bekannt ist.) |
 |
Band-Band-Übergänge zeichnen wir zukünftig auch im einfachen Banddiagramm
nur noch senkrecht nach oben – und nach unten. Denn alles, was wir bisher gelernt
haben, gilt selbstverständlich nicht nur für die Schaffung eines Elektron-Loch-Paares durch den Übergang
eines Elektrons vom Valenz- ins Leitungsband, sondern auch für die Rekombination, die Wiedervereinigung von Elektron und Loch.
|
|
 |
Versuchen wir, das im obigen Bild einzutragen, bekommen wir ein Problem:
Nach der Thermalisierung von Elektron und Loch sitzen sie im gezeichneten Beispiel nicht mehr senkrecht
übereinander! Ein Übergang nach unten und damit Rekombination ist ohne Verletzung des Kristallimpulserhaltungssatzes
nicht möglich! |
|
Direkte und indirekte Halbleiter |
| |
 |
Der entscheidende Punkt ist, daß es in einem reduzierten Banddiagramm ganz
generell genau zwei Möglichkeiten für die Bandkanten gibt, durch welche die fundamentale Bandlücke definiert
wird: |
|
 |
1.) Das Maximum des Valenzbandes sitzt im k-Raum
genau unter dem Minimum des Leitungsbandes. |
|
 |
2.) Das Maximum des Valenzbandes und das Minimum des Leitungsbandes liegen bei verschiedenen
k-Werten. |
 |
Wir schauen uns mal an, wie das (schematisch) in realen
Materialien aussieht: |
| |
|
|
 |
In der oberen Reihe sind Minima und Maxima übereinander; wir nennen Materialien mit
dieser Eigenschaft direkte Halbleiter. Das freie Elektronengas als Referenz gehört
formal auch dazu. |
|
 |
Die untere Reihe zeigt indirekte Halbleiter (wir
zählen Diamant mal dazu, obwohl das eigentlich ein Isolator ist). Man beachte, daß auch Germanium ein indirekter
Halbleiter ist, denn Maximum und Minimum liegen eben nicht beim selbem k-Wert
und lassen sich auch nicht durch Addition oder Subtraktion von reziproken Gittervektoren untereinander bringen. |
 |
Wie kommt man darauf? Kann man denn einem Halbleiter "ansehen", ob er
eine direkte oder indirekte Bandlücke hat? |
|
 |
Im Prinzip ja: Man muß nur schauen, wie sich die Lichtabsorption als Funktion der Frequenz
bzw. Wellenlänge (d. h. der Farbe des Lichtes) verhält. Setzt sie bei einer bestimmtem Frequenz bzw. Wellenlänge
schlagartig und kräftig ein, handelt es sich um einen direkten Halbleiter. Denn sobald hn = Eg,
wird Absorption möglich. |
|
 |
In einem indirekten Halbleiter kann bei hn = Eg
nicht kräftig absorbiert werden, denn es gibt bei dieser Energie ja keine unmittelbare Impulserhaltung. Erst bei höheren
Photonenenergien, die hn = Edirekt entsprechen, dem direkten
Übergang mit der kleinsten Energie, wird die Absorption kräftig einsetzen. Im Bereich zwischen Eg
und Edirekt wird zwar auch absorbiert (über einen "Umweg"), aber nur schwach. |
|
 |
Dieser Unterschied wirkt sich auf den Absorptionskoeffizienten a
aus; a ist definiert über die exponentielle Abschwächung von Licht beim Durchdringen
des Materials: Je größer a, desto geringer die Eindringtiefe des Lichtes. |
|
 |
Hier ein paar Beispiele für Messungen (vor allem mit infrarotem Licht) der Wellenlängenabhängigkeit
von a bei einigen Materialien; man beachte die Form der jeweiligen "Absorptionskante": |
| |
|
|
 |
Si und Ge sind die einzigen indirekten Halbleiter in diesem Diagramm, man sieht
den weichen Einsatz der Absorption sehr deutlich. Beim Germanium sieht man darüber hinaus den Einfluß der direkten
Bandlücke, die bei etwas höherer Energie liegt (siehe die obige Bandstruktur; beim Silizium "funktioniert"
das nicht, weil dort höher im Leitungsband kein lokales Mininmum vorliegt). |
 |
Damit soll's erst mal genug sein; wir werden später auf dieses Thema zurückkommen.
|
| |
Zu diesem Abschnitt gibt es derzeit weder eine Übungsaufgabe noch schnelle Fragen.
|
© H. Föll (MaWi für ET&IT - Script)