7.1.2 Dia-, Para- und Ferromagnetismus

Feld, Fluß, Permeabilität und magnetische Suszeptibilität

Im großen und ganzen sind die magnetischen Begriffe analog zu den elektrischen; wir können uns also kurz fassen.
Da man sie nicht grundsätzlich als eine Konsequenz magnetischer Ladungen definieren kann, haben wir zunächst eine empirisch definierte magnetische Feldstärke H .
Zur Erzeugung des Magnetfeldes jagen wir den Strom der Stärke I durch eine Spule der Länge s mit Zahl der Windungen=n. Im Inneren der Spule gilt dann:
H  =  I · n
s
Das ist zwar keine sehr befriedigende Definition, aber was soll's. Die Einheit von H ist damit: [H]=1 A/m
Im Vakuum gilt für die Beziehung zwischen Magnetfeld H und der magnetischen Flußdichte (kurz: magnetischer Fluß) oder der magnetischen Induktion B, dem Analogon der Verschiebungsdichte D:
B   =  µo · H
Dabei ist µ o=magnetische Permeabilität des Vakuums=4p · 10–7 Vs/Am=1,26 · 10–6 Vs/Am.
Die Einheit von B ist: [B]=1 Vs/m2. Dabei ist 1 Vs/m2=1 Tesla
103/4p  A/m waren früher bei der Feldstärke 1 Oersted. 1 heutiges Tesla waren mal bei der Flußdichte 104 Gauss im alten (und in manchen Aspekten besseren) System.
Warum man den berühmten Mathematiker und Wissenschaftler Gauss dem Abenteurer und Wirrkopf Tesla geopfert hat, läßt sich nur politisch, also unlogisch erklären.
In Anwesenheit eines Materials (in der gedanklichen Spule) erhalten wir
B  = µo · µr· H
Dabei ist µr =relative Permeabilität des Materials – in vollständiger Analogie zur elektrischen Flußdichte und der Dielektrizitätskonstante. Auch µr ist eine dimensionslose Zahl.
Wir teilen den Fluß wiederum in den externen Fluß im Vakuum plus den Anteil des Materials und schreiben
B =  µo · H +  J
J ist dann offenbar die magnetische Polarisation in kompletter Analogie zum dielektrischen Fall. (Und das gilt, wie wir noch sehen werden, weitestgehend auch für die ihr zugrundeliegende Physik.)
Im Magnetismus macht man sich das Leben schreib- und rechentechnisch noch einfacher durch Einführung der Magnetisierung M wie folgt:
M  =  J 
µo 		      
     
B  =  µo · (H + M)
Damit haben wir wiederum als (vermutetes) Materialgesetz
M  =  (µr – 1) · H
     
M  =:  c mag · H
Die Berechnung der magnetischen Suszeptibilität cmag =(µr – 1) wird damit zur vordringlichen materialwissenschaftlichen Aufgabe.
Da wir die magnetischen Polarisierungsmechanismen schon (oberflächlich) angeschaut haben, geht das ganz schnell.
 

Dia-, Para- und Ferromagnetismus

Zunächst die Schlüsselfrage: Nenne ein elektro- oder informationstechnisches Produkt, bei dem es darauf ankommt, daß ein (nicht-ferromagnetisches) Material dia- oder paramagnetisch ist.
Richtig! Es kommt nicht darauf an. Also machen wir es kurz:
Zuerst die diamagnetischen Materialien:
Diamagnetische Materialien
Magnetisches Moment Nein
Reaktion auf externes Feld Magnetische Momente werden induziert (durch kleine Störungen des "Umlaufs" der Elektronen).
Die induzierten magn. Momente schwächen das Feld, d. h. cmag < 1.
Keine Temperaturabhängigkeit. 		Diamagnetism
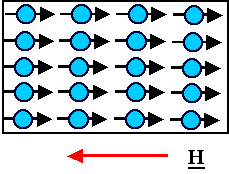
Die schwarzen Pfeile sind ganz kurz!
Wert von µr µr £»1.
Sehr kleiner Effekt in regulären Materialien 		Aber:
µr=0
in Supraleitern
(idealer Diamagnet)
Typische Materialien Alle Elemente mit gefüllten Orbitalen (immer gerade Ordnungszahl) Alle Edelgase und z. B. H2, Cu, H2O, NaCl, Bi, ...
Alkalimetall- oder Halogenionen
Jetzt schauen wir auf Materialien, bei denen mindesten eine der beteiligten Atomsorten ein magnetisches Moment mit sich herumschleppt. Wir unterscheiden zwei Grenzfälle:
1. Starke interne Wechselwirkung zwischen den magnetischen Momenten. Das bedeutet im Klartext: Die Energie (oder das Potential) der Wechselwirkung ist deutlich größer als kBT, die thermische Energie. Dann erhalten wir Ferromagnetismus.
2. Keine Wechselwirkung oder zumindest Wechselwirkungsenergie < kBT. In diesem Fall haben wir paramagnetische Materialien.
Der erste Fall wird dann oberhalb einer Grenztemperatur, genannt Curietemperatur TC, automatisch in den 2. Fall übergehen.
Eine schematische Klassifizierung sieht so aus:
Paramagnetische und ferromagnetische Materialien
Magnetisches Moment Ja
Interne Wechselwirkung Stark (>> kBT)  ÞFerromagnet Schwach (<< kBT) Þ Paramagnet
Geordnete Bereiche Ja Nein
Es gibt viele Möglichkeiten der Ordnung; im Bild unten sind einige gezeigt.
Wichtig sind
  • Ferromagnete (meist Leiter)
  • Ferrimagnete (meist Isolatoren)
Sie haben große lokale Nettomomente

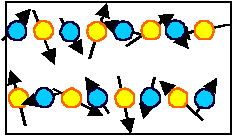
Ein paramagnetisches Material:
Ungeordnete magnetische Struktur, Momente fluktuieren zeitlich.
Im Mittelwert über Zeit und Ort kein Nettomoment
Reaktion auf externes Feld Großes magnetisches Moment in Feldrichtung bei Ferro- und Ferrimagnetismus Kleiner Nettoeffekt in Feldrichtung;
Mechanismus vollständig analog zur Orientierungspolarisation der Dielektrika.
Wert von µr µr >> 1
für Ferromagnete
µr > 1
für Ferrimagnete
µr » 1
for Anti-Ferromagnete 		µr ³» 1
T-Abhängigkeit Paramagnetisch oberhalb Curie-Temperatur Nur schwache T-Abhängigkeit.
Typische Materialien
(mit TC)		 Ferro:
Fe (770 oC), Co (1121 oC), Ni (358 oC), Gd (16 oC )
Ferri:
"AlNiCo", Co5Sm , Co17Sm2 , "NdFeB"
Fe3O4 , ...
Anti-Ferro:
Cr (308 oC ), MnO (116 oC ), NiO (525 oC), ... 		Mn, Al, Pt, O2 (Gas und flüssig), ...
Mutter Natur läßt sich bei Ordnungen einiges einfallen. Im Bild unten sind schematisch nur die drei wichtigsten gezeigt – und, zum Spaß, noch die "frustrierte Struktur" bei Antiferromagneten in z. B. einem bcc-Kristall (die "frustrierten" Momente, die es nicht allen Nachbarn recht machen können, sind rot gezeichnet).
Es gibt noch viel mehr (und viel kompliziertere) Ordnungsstrukturen, mit denen sich durchgeknallte Physiker und Materialwissenschaftler amüsieren. Die meisten haben aber wie die Anti-Ferromagnete kein Nettomoment und sind deshalb (noch) technisch unwichtig.
Magnetische Ordnung
Wir müssen uns merken:
  • Die einzigen bei sinnvollen Temperaturen ferromagnetischen Elemente sind Fe, Co und Ni. (Mn hätte es fast "geschafft", es reichte aber nicht ganz.)
  • Cr ist das paradigmatische antiferromagnetische Element. Damit ist es zwar als Element magnetisch "nutzlos", aber es hat immerhin eine starke Wechselwirkung zwischen seinen Dipolen. Kein Wunder also, daß man es in magnetischen Legierungen findet.
  • Es gibt viele und oft exotisch anmutende magnetische Legierungen und Verbindungen – z. B. die extrem starken Dauermagnete Nd2Fe14Bor Sm2Co 17. Hier handelt es sich dann um technisch sehr wichtige Werkstoffe der ET&IT-Technik!
Viel mehr wollen wir über die Grundlagen gar nicht wissen. Wir schauen uns jetzt nur noch einige wichtige Eigenschaften der Ferromagnete an.
 
Jetzt noch die schellen Fragen:
Fragebogen
Schnelle Fragen zu 7.1.2
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi für ET&IT - Script)