6.4.4 Gesamtschau

Die komplette dielektrische Funktion

Was hier kommt haben wir in Prinzip schon gehabt oder brauchen wir nicht zu wissen.
   
Die komplette dielektrische Funktion eines Dielektrikums ist eine Überlagerung aller beteiligten Mechanismen. Für ein fiktives Material, das alle Mechanismen in Reinkultur enthielte (und das es nicht mal annähernd gibt), sähe das so aus:
Complete frquency dependence of epsilon
Das Bild zu zeigen hat einen gewissen Wert: Es ist seit undenklichen Zeiten in dieser Form in allen Standardlehrbüchern gedruckt.
Immer beachten, dass die Frequenz auf einer log Skala aufgetragen ist!
Kramers - Kronig Beziehungen
   
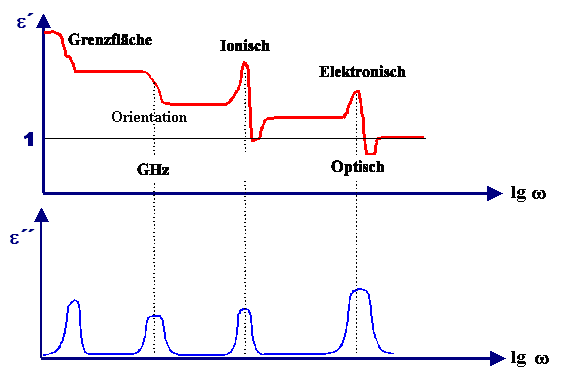
Was auffällt ist, dass Real- und Imaginärteil irgenwie korreliert zu sein scheinen. Das ist ja auch nicht überraschend, beide "codieren" ja das dielektrische Verhalten ein-und-desselben Materials.
In der Tat steckt die gesamte verfügbare Information schon in einer der beiden Kurven. Kennt man eine - den Real- oder Imaginärteil, das ist egal - kann man die andere ausrechnen.
Das ist eine allgemeine mathematische Eigenschaft komplexer Funktionen, die eine physikalische Realität beschreiben. Die Beziehung zwischen Real- und Imaginärteil heißt Kramers- Kronig Beziehung
Die Kramers-Kronig Beziehung sieht so aus
e'( w)  =   – 2 w
p 		   ¥
ó
õ
0		   w* · e''(w*)
w*2– w2 		· dw*

e ''(w)  =   2 w
p
    ¥
ó
õ
0		   e'(w*)
w*2– w2 		· dw*  
Es gibt halt nichts praktischeres als eine gute Theorie! Der Praktiker spart sich damit die Messung einer der beiden Kurven!
 
Nochmals Verluste im Dielektrikum
   
Wir hatten uns schon klar gemacht, dass die Wirkleistung, die das Dielektrikum aufwärmt, durch die folgende Gleichung gegeben ist:
LW   =  w · e'' · E2 
LW ist also direkt proportional zum Imaginärteil der dielektrischen Funktion. Und dabei ist es egal , woher der Imaginärteil kommt!
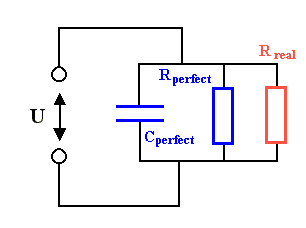
Das bedeutet: Selbst "ideale" Dielektrika (= ideale Isolatoren) sind in bestimmten Frequenzbereichen verlustbehaftet. Kommt dazu außerdem noch ein nicht ideales Verhalten in Form einer gewissen DC Leitfähigkeit, haben wir jetzt folgendes Gesamtersatzschaltbild:
Equivalent circuit diagram of a real dielectric
stotal  =  sperfect  +  sreal
     
   =  sDK  +   s0 
Rperfect (besser s perfect) charakterisiert den Verlustwiderstand des idealen Dielektrikums, s real den nicht-idealen Teil
Für parallel geschaltete Widerstände können wir die Leitfähigkeiten einfach addieren (mit den Widerständen addiert man die Kehrwerte). Da man in der Praxis nicht auseinanderhalten kann, welcher Teil ideal und welcher real ist, nimmt man einfach die Summe s total . Damit haben wir:
e''  =  stotal
w
Wir haben nirgendwo vorausgesetzt, dass sreal klein sein muss; es kann eine x-beliebiege Leitfähigkeit oder Widerstand sein.
Damit enthält die komplexe dielektrischen Funktion jetzt das gesamte dielektrische Verhalten eines beliebigen Materials!
Zum Verständnis müssen wir aber noch die Mechanismem der Leitfähigkeit behandeln - in Modul 9
   
Jetzt noch ein paar schnelle Fragen:
Fragebogen
Schnelle Fragen zu 6.4.4
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi für ET&IT - Script)