|
Uns interessieren Frequenzen bis in Ultraviolette - d. h. jenseits 1015
Hz. | |
|
|
 |
Die Grundbeziehung ist Þ |
|
|
 |
Wie Eingang und Ausgang aussieht, hängt von der Frequenz ab. |
|
|
 |
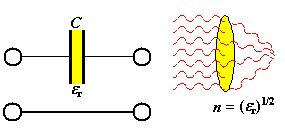
Bei optischen Frequenzen wird man z. B. Licht durch eine Linse schicken, bei RF reicht es, einen Kondensator
zu vermessen. | |
|
| |
| |
 |
Es gibt nur zwei grundlegende Mechanismen, die die Frequenzabhängigkeit der
DK bestimmen: | |
|
|
 |
Elektronenpolarisation und ionische Polarisation zeigen Resonanz
; die Orientierungspolarisation zeigt Relaxation. |
|
| |
| |
| |
 |
Resonanz erhält man beim getriebenen gedämpften Schwinger. |
|
| m · |
d2x
dt2 |
+ mkR · |
dx
dt |
+ kF · x |
= |
q · E0 · cos(wt)
|
|
|
|
 |
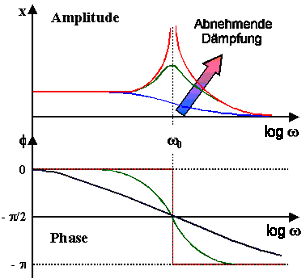
Die Lösungen kann man als Amplitude und Phase oder als Real- und Imaginärteil einer
komplexen Amplitude darstellen | |
|
 |
Die Amplitude bestimmt das elektrische Dipolmoment, da in beiden Resonanzmechanismen die Ladungen
gegeneinander schwingen. | |
| | |
| |
|
 |
Die Darstellung der Lösung sieht dann so aus; wir nehmen natürlich die
komplexe Variante | |
|
|
| |
|
|
|
| |
|
| | |
| |
|
|
 |
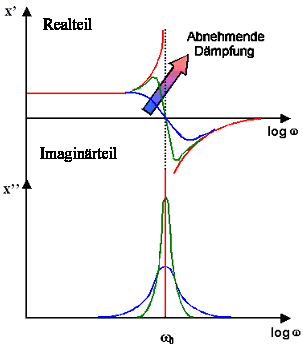
Damit ist der Verlauf der komplexen DK im Bereich der Resonanzen grundsätzlich
skizziert | | |
| | |
| |
 |
In allen Materialien muss die Resonanz stets stark gedämpft sein, da die
die Energie eines heftig schwingenden Dipols sofort auf Nachbarn dissipiert wird. |
| |
| | |
| |
 |
Die Resonanzfrequenz w
0 ist gegeben durch Þ |
|
| w0' | = |
æ
ç
è | kF
m |
ö
÷
ø | 1/2 |
|
|
|
 |
In der Federkonstante der ionischen Polarisation steckt der E-Modul. Es schwingen
"schwere" Atome, und wir wissen schon, dass w0
» 1013. | |
|
 |
Bei der Atom- oder Elektronenpolarisation schwingen leichte Elektronen, daher w
0 » 1015 d.h. im optischen Bereich. |
|
| |
| |
| |
 |
Die Relaxation, d.h. allmähliche Rückkehr
aus dem etwas orientierten Zustandes nach Abschalten des Feldes in den völlig ungeordneten Zustand, wird beschrieben
durch Þ | |
|
|
 |
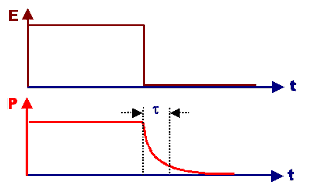
Aus der Grundgleichung in der Zeit, die das "Abschalten" beschreibt, |
|
|
| |
|
|
|
| P(t) | = |
P0 · exp( –t / t ) |
|
| |
|
| |
| |
| |
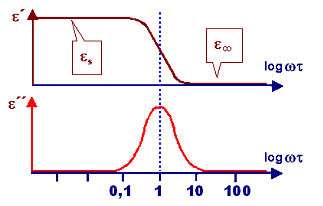
folgt die Grundgleichung in der Frequenz durch Fourier-Transformation. Der Graph dazu sieht
so aus Þ | |
|
|
 |
Der typische Wert der Relaxationszeitkonstante t liegt
im Bereich 1/t » 10 GHz. |
|
|
 |
Insbesondere der Imaginärteil erklärt die Funktionsweise der "Mikrowelle". |
|
© H. Föll (MaWi für ET&IT - Script)