6.5 Optik mit komplexem Brechungsindex

6.5.1 Was man wissen möchte und was man wissen kann

Die Bilder unten zeigen schematisch und relativ komplett, was man über das Verhältnis von Licht und Materie gerne wissen möchte.
Die wesentlichen Daten über sichtbares Licht finden sich im Link. Hier nehmen wir nur mal die Zahlen, die man wissen sollte zur Kenntnis:
Zahlen zum Licht
  Zehnerwert Besserer Wert
Wellenlänge  »  1 µm 500 nm
Frequenz  »  10 14Hz 5 · 10 14Hz
Energie  »  1 eV 2,5 eV
Frequenz n und Wellenlänge l sind über die Lichtgeschwindigkeit c=c0/n (c0 =Lichtgeschwindigkeit im Vakuum » 3 · 108 m/s; n=Brechungsindex) immer verknüpft durch die "Dispersionsrelation":
c  =  n · l
Was im Großen und Ganzen passieren kann ist:
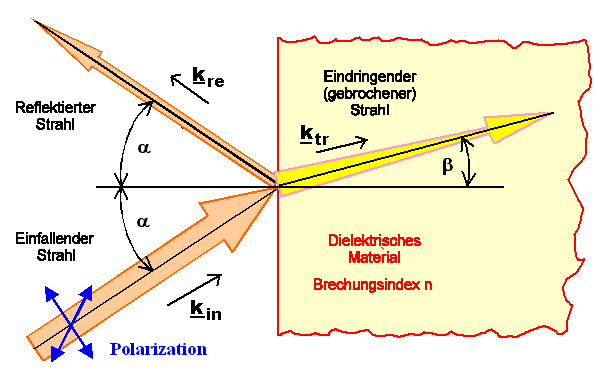
Ein Lichtstrahl mit einer Intensität I0 (symbolisiert durch die Breite des Pfeils im Bild unten), der Kreisfrequenz w und einer definierten optischen Polarisation Popt (d. h. Schwingungsebene des elektrischen Feldes) fällt unter einem Winkel a auf ein Material.
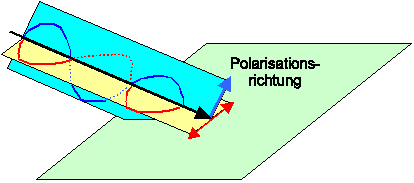
Die optische Polarisation Popt kann immer aufgeteilt werden in einen Anteil in der Ebene des Materials und einen Anteil senkrecht dazu, wie im unteren Bild gezeigt.
Optical beams and material
Polarization and reflection
Was passieren kann ist:
  1. Ein Teil IM des einfallende Lichts wird gebrochenund dringt unter dem Winkel b in das Material ein.
  2. Der Teil R=I0 – IM des einfallenden Lichtes wird unter dem Winkel –a reflektiert .
  3. Das im Material laufende Licht wird absorbiert: IM(z)=IM(z=0) · exp(–az) . 1/a = a–1 ist die Absorptionslänge, deren Zahlenwert angibt, nach welcher Strecke die Intensität auf 1/e=0,368 abgeklungen ist
Was wir gerne wissen, d.h. ausrechnen möchten ist
  1. Der Reflexionskoeffizient R;
  2. Der (Brechungs)winkel b;
  3. Der Absorptionskoeffizient a,
 immer als Funktion des Einfallwinkels a, der Polarisation Popt und der Kreisfrequenz w oder "Farbe" des Lichts. Mehr kann man für die Grundzüge der Optik eigentlich gar nicht wissen.
 
Überraschung! Die Antworten zu allen obigen Fragen stecken komplett in der dielektrischen Funktion des Materials!
Wir müssen lediglich auch den Brechungsindex als komplexe Größe begreifen: n* =  n + i · k (statt n' und n'' bevorzugen wir hier n und k). Wir haben dann die folgenden Relationen:
(n + ik )2  =  e ' - i · e''

n2  =  1
2		 æ
ç
è 		æ
è 		e' 2  + e'' 2  ö
ø 		½   +   e' ö
÷
ø

k2  =  1
2		 æ
ç
è 		æ
è 		e' 2  + e'' 2 ö
ø 		½   –  e' ö
÷
ø
Für e''=0 erhalten wir sofort n2=e'; k=0.
Im n stecken die Antworten auf die Fragen 1 und 2, im k die Antwort auf Frage 3.
Antwort auf die Fragen 1 und 2 geben die sogenannten Fresnel-Gleichungen, die wir uns aber hier ersparen.
Wie ist das mit der Absorption?
Wenn man kurz rechnet, sieht man, dass die Feldstärke und damit auch Intensität der im Material laufenden elektromagnetischen Lichtwelle mit exp(–w · k · x/ c) abfällt; unten ist der Rechengang gezeigt (dabei berücksichtigen, dass die Lichtgeschwindigkeit im Material durch c/n gegeben ist)
Ex  =    E0, x · exp [ i · æ
ç
è 		w· n*
c 		 · x –  w· t ö
÷
ø 		]  =    E0, x · exp [i ·   æ
ç
è 		w · (n  +  i · k)
c 		 · x  –   w · t  ö
÷
ø 		]

Ex  =    E0, x · exp [ æ
ç
è 		i · w · n· x
c 		 –   w · k · x
c 		 –  i · w · t  ö
÷
ø 		]=   exp ( –    w · k· x
c  		  ) ·  exp[ i · (kx · x  –   w · t)]
Damit gilt für den Absorptionskoeffizienten a=wk/c=2p k/l (wir haben immer c= n · l) und also 2p k=al=l/a –1 . Die Zahl k sagt daher effektiv aus, nach wievielen Wellenlängen das Licht weitgehend absorbiert ist.
 
Das soll zur Optik erst mal reichen.
Wichtig ist zunächst mal nur, zu verstehen, daß bei optischen Frequnzen nichts grundsätzlich Neues entsteht. Wir haben die Interaktion eines elektrischen Felds mit einem Dielektrikum.
Jetzt noch ein paar schnelle Fragen:
Fragebogen
Schnelle Fragen zu 6.5.1
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi für ET&IT - Script)