Lösung zur Übung 2.3-1

Eigenschaften der Fermiverteilung

1. Zeige, daß das Aufweichungsintervall der Fermieverteilung in etwa den Wert 4kT hat.
Die Ableitung der Fermieverteilung nach der Quotientenregel ergibt unmitelbar
df(E, T)
dE		   =  – 1
kT		 exp(..)
{exp(..) + 1}2
Für E = EF wird der Exponent = 1 und wir bekommen
 
df(E = EF, T)
dE 		   =  – 1
4kT
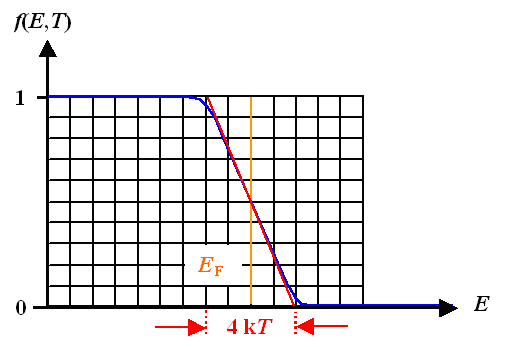
Ersetzen wir die Fermiverteilung um EF durch eine Gerade mit der Steigung –(1/4kT), definiert sie gerade ein Aufweichungsintervall von 4kT wie unten gezeigt.
Aufweichungszone der Fermiverteilung
   
2. Zeige, daß für E >> EF die Boltzmannnäherung gilt.
Für E >> EF und (E – EF) >> kT steht im Exponent eine Zahl >> 1
Damit ist exp(E – EF)/kT  >>  1 und die +1 im Nenner kann vernachlässigt werden. Man erhält
f(E >> EF, T)   »  1  
exp(E – EF)/kT		   =   exp– (E – EF)/kT
Das ist die Boltzmannverteilung!
 

Mit Frame Mit Frame as PDF

gehe zu Verifikation des Lösungsansatzes

gehe zu Übung 2-9

gehe zu Übung 2.4-1 Defekte und mittlere freie Weglänge

gehe zu Übung 2-9

© H. Föll (MaWi 2 Skript)