3.16 Fourier Transformation: Solving DEQs

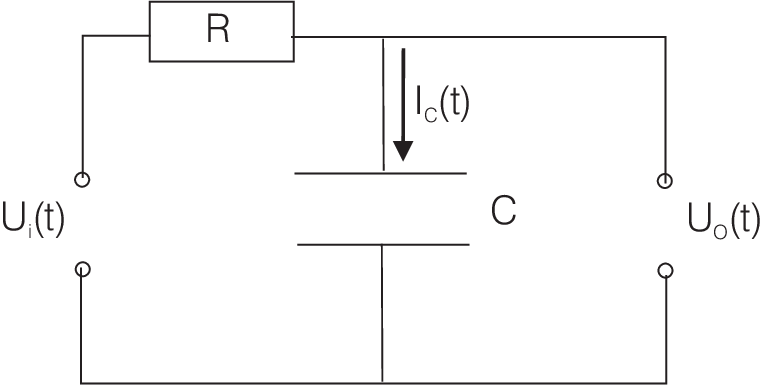
Example 1: Low pass filter:

We know: \begin{eqnarray*}U(t) &=& R\; I(t) \mbox{\quad(resistor)}\\ U(t)&=&\frac{Q(t)}{C} \mbox{\quad(capacitor).}\end{eqnarray*}

So according to the Kirchhoff equations we find for the current across the capacitor \(I_C\)

After Fourier-Transformation this differential equation for \(U_o\) translates into

i.e. 

which is the response to a sinusoidally modulated input signal with frequency \(\omega/2\pi\). Using the example IV for calculation of Fourier transformed we can find the original function \(A(t)\) of \(A(\omega)\) \begin{eqnarray*}A(t) &=& \F^{-1}\left\{\frac{1}{1+i \omega RC}\right\}\\ &=&\frac{\sqrt{2\pi}}{RC}\F^{-1}\left\{\frac{1}{\sqrt{2\pi}}\frac{1}{\frac{1}{RC}+i \omega }\right\} = \left\{\begin{array}{cl}\frac{\sqrt{2\pi}}{RC}e^{-\frac{t}{RC}}&\mbox{for $t\ge 0$}\\0&\mbox{for $t\lt0$}\end{array}\right.\end{eqnarray*}

According to the convolution theorem we find \begin{eqnarray*}U_o(t) & = & \F^{-1}\left\{\frac{1}{1+i \omega RC} U_e(\omega)\right\}\\ &=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}A(t-\tau)\;U_i(\tau)\;d\tau = \frac{1}{RC} \int\limits_{-\infty}^{t}e^{-\frac{t-\tau}{RC}}\;U_i(\tau)\;d\tau\end{eqnarray*}

So this integral allows to calculate the response \(U_o(t)\) of a low pass filter to an arbitrary input signal \(U_i(t)\). Typically a filter is characterized in real space by the response to a step like perturbation

\[U_i(t)=\left\{\begin{array}{cl}U_0&\mbox{for $t\ge 0$}\\0&\mbox{for $t\lt0$}\end{array}\right.\quad,\] which for our case is \begin{eqnarray*}U_o(t) & = & \frac{1}{RC} \int\limits_{0}^{t}e^{-\frac{t-\tau}{RC}}\;U_0\;d\tau\\ & = &U_0 \left(1-e^{-\frac{t}{RC}}\right) \end{eqnarray*}

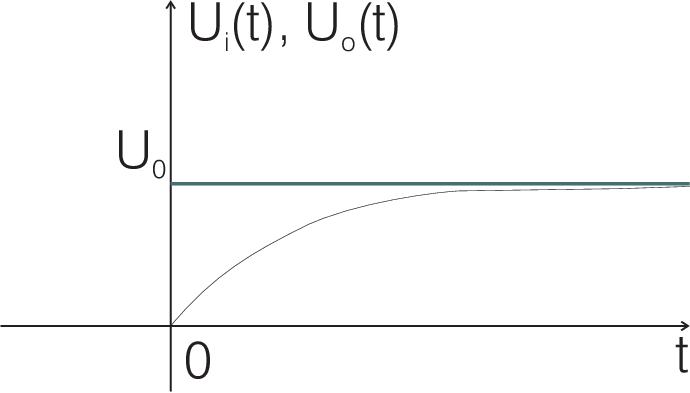
• the transfer function \(A(\omega)\) in Fourier space

• the answer to a step like perturbation in real space, i.e. the transient.

© J. Carstensen (Math for MS)