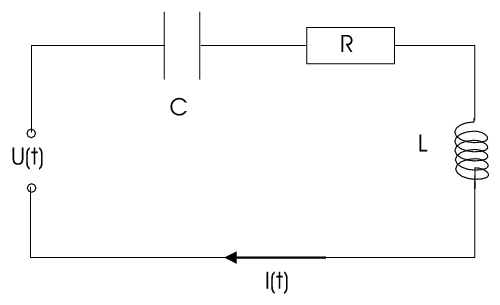
We know: \begin{eqnarray*}U(t) &=& R I(t) \mbox{\quad(resistor)}\\ U(t)&=&\frac{Q(t)}{C} \mbox{\quad(capacitor)}\\ U(t)&=&L\dot{I}(t)
\mbox{\quad(inductance).}\end{eqnarray*}
| 
|
We know: \begin{eqnarray*}U(t) &=& R I(t) \mbox{\quad(resistor)}\\ U(t)&=&\frac{Q(t)}{C} \mbox{\quad(capacitor)}\\ U(t)&=&L\dot{I}(t)
\mbox{\quad(inductance).}\end{eqnarray*}
| 
|
Voltages add up in series, so we get
| \[\ddot{I}(t)+2\gamma\dot{I}(t)+\omega_0^2I(t)=\frac{1}{L}\dot{U}(t)\qquad\begin{array}{ccl}\omega_0^2&=&\frac{1}{LC}\\\\2\gamma&=&\frac{R}{L}\end{array}\] |
This is a linear inhomogeneous DEQ with constant coefficients. Solution:
Solving the homogeneous equation by an exponential approach.
Solving the inhomogeneous solution by Fourier Transform of left and right side, i.e.
\begin{eqnarray*}\frac{1}{L}\dot{U}(t)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\tilde{U}(p)e^{ipt} dp\\ I(t)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\tilde{I}(p)e^{ipt}dp\end{eqnarray*}
\begin{eqnarray*}\Rightarrow\;\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\left\{-p^2+2\gamma ip+\omega_0^2\right\}\tilde{I}(p)e^{ipt}dp&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\tilde{U}(p)e^{ipt} dp\\ \Rightarrow\;\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\underbrace{\left\{\left(-p^2+2\gamma ip+\omega_0^2\right)\tilde{I}(p)-\tilde{U}(p)\right\}}_{\mbox{\normalsize 0}}e^{ipt}dp&=&0\end{eqnarray*}
\begin{eqnarray*} \Rightarrow\;\tilde{I}(p)&=&\underbrace{\frac{1}{-p^2+2\gamma ip+\omega_0^2}}_{\mbox{\normalsize $\tilde{A}(p)$}}\tilde{U}(p)=\tilde{A}(p)\tilde{U}(p)\\ \rightarrow\,I(t)&=&\F^{-1}\left\{\tilde{A}(p)\tilde{U}(p)\right\}=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\frac{1}{L}\dot{U}(t')A(t-t')dt'\\ \mbox{Thus only \quad} A(t)&=&\F^{-1}\left\{\frac{1}{-p^2+2\gamma ip+\omega_0^2}\right\} \mbox{\quad must be calculated}\\ \mbox{Quite obviously we get} &&\quad \frac{1}{-p^2+2\gamma ip+\omega_0^2}=\frac{-1}{(p-i\gamma)^2+(\gamma^2-\omega_0^2)}\\ \mbox{and \quad}F(p+a)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}f(x) e^{-i(p+a)x}dx=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\left(f(x)e^{-iax}\right)e^{-ipx} dx\\ \mbox{We already prooved \quad} \F \left\{e^{-\alpha|x|}\right\}&=&\sqrt{\frac{2}{\pi}}\frac{\alpha}{p^2+\alpha^2}\\ & & \\ \mbox{and finally get:} & & \\ & & \\ \F^{-1}\left\{\frac{-1}{(p-i\gamma)^2+(\gamma^2-\omega_0^2)}\right\}&=&-e^{-i(-i\gamma)t}\frac{1}{\sqrt{\gamma^2-\omega_0^2}}\sqrt{\frac{\pi}{2}}e^{-\sqrt{\gamma^2-\omega_0^2}|t|}\;\mbox{ for $\gamma\neq \omega_0$}\\ \Rightarrow\,A(t)&=&-\sqrt{\frac{\pi}{2}}\frac{1}{\sqrt{\gamma^2-\omega_0^2}}e^{-\gamma t-\sqrt{\gamma^2-\omega_0^2}|t|}\\ \Rightarrow\,I(t)&=&-\frac{1}{2\sqrt{\gamma^2-\omega_0^2}}\int\limits_{-\infty}^{+\infty}\frac{1}{L}\dot{U}(t')e^{-\gamma (t-t')}e^{-\sqrt{\gamma^2-\omega_0^2}|t-t'|}dt' \end{eqnarray*}
If \(U(t) = 0\) for \(t\lt0\) than \(\dot{U}(t) = 0\) for \(t\lt0\) and the above equation simplifies to
| \[I(t) = -\frac{1}{2\sqrt{\gamma^2-\omega_0^2}}\int\limits_{0}^{+\infty}\frac{1}{L}\dot{U}(t')e^{-\gamma (t-t')}e^{-\sqrt{\gamma^2-\omega_0^2}(t-t')}dt'\] |
which by partial integration can be transformed into
| \[I(t) = \frac{\gamma+\sqrt{\gamma^2-\omega_0^2}}{2 L \sqrt{\gamma^2-\omega_0^2}}\int\limits_{0}^{+\infty}U(t')e^{-\gamma (t-t')}e^{-\sqrt{\gamma^2-\omega_0^2}(t-t')}dt'\] |
As we already see from this last equations the real problem are the start values! It is not really simple to solve. What we have calculated up to now is a solution of the inhomogeneous differential equation. Since we are dealing with a linear differential equation we can still add any solution of the homogeneous differential. We will discuss this with the Laplace Transform. Another possibility to solve such differential equations are Greens Functions.
![]() Fourier Transformation: Solving DEQs
Fourier Transformation: Solving DEQs
© J. Carstensen (Math for MS)