 |
Factorial function: \(n!=1\cdot2\cdot3\cdot4\cdot\ldots\cdot n\)
Thus: \begin{eqnarray*}n!&=&n\cdot(n-1)! \qquad\mbox{ and definition for convenience}\\
(n+1)!&=&(n+1)n!\qquad 0!=1\\ n!&=&n(n-1)!=n(n-1)\cdot(n-2)!\end{eqnarray*}
only defined
for natural numbers \(n\ge 0\).
This will now be generalized for real values.
Consider:
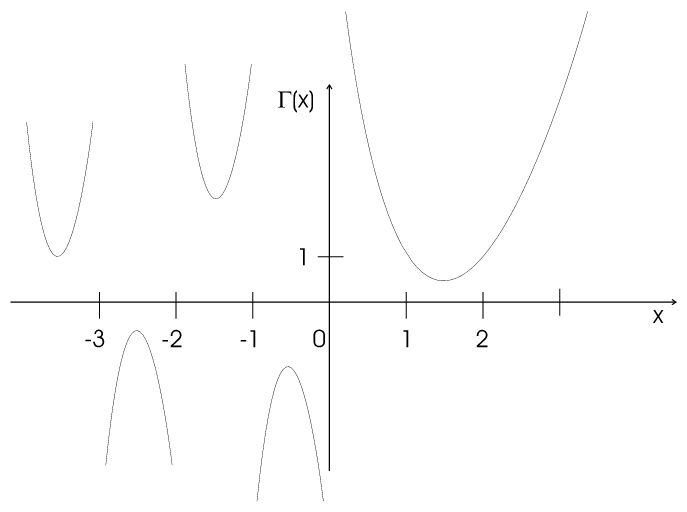
| \[\Gamma(x)=\int\limits_0^\infty e^{-t}t^{x-1}dt\qquad \mbox{for }x\gt0\] |
Than it is simple to show that \(\Gamma(n+1)=n!\;\;\) for \(n=0,1,2,3,\ldots\)
| \[\left(\int\limits_0^\infty e^{-t}t^n dt=n!\right)\] |
\(\Rightarrow\) Function \(\Gamma(n)\) is equivalent to \((n-1)!\) for natural numbers \(n\). \begin{eqnarray*}\Gamma(x+1)=\int\limits_0^\infty e^{-t}t^x dt&=&-e^{-t}\left.t^x\right|_0^\infty+\int\limits_0^\infty e^{-t}xt^{x-1}dt=x\Gamma(x)\\ \mbox{Thus:}\;\Gamma(x+1)=x\Gamma(x)&=&x\cdot(x-1)\Gamma(x-1)=x(x-1)(x-2)\Gamma(x-2)= ...\end{eqnarray*}
Same property as factorial but not restricted to integer numbers. The \(\Gamma\) function exists for real numbers, except for negative integers and zero, since
| \[\Gamma(x+1) = x \Gamma(x) \quad \Rightarrow \quad 1 = 0! = \Gamma(1) = 0 \Gamma(0),\] |
i.e \(\Gamma(0)= \infty\) and thus \(\Gamma(n)= \infty\) for negative integers.
 |
Special values:
| \[\Gamma(\frac{1}{2})=\int\limits_0^\infty e^{-t}\frac{1}{\sqrt{t}}dt=2\int\limits_0^\infty e^{-t^2}dt=\sqrt{\pi}\] |
Stirling Formula: An asymptotic approximation for the factorial function one gets by calculating the Taylor approximation up to quadratic order of
| \[g(x) = \ln\left( x^n \exp(-x)\right) = n \ln x - x \qquad ,\] |
i.e.
| \[\frac{dg}{dx} = \frac{n}{x} - 1 \qquad \mbox{ and } \qquad \frac{d^2g}{dx^2} = -\frac{n}{x^2} \lt 0 \] |
around it’s maximum at \( x_0 = n\).
We find
| \[g(x) \approx g(x_0) + \frac{dg}{dx}(x_0) (x-x_0) + \frac{1}{2}\frac{d^2g}{dx^2}(x_0) (x-x_0)^2 = n \ln n -\frac{(x-n)^2}{2 n} \] |
finally giving
| \[n! = \int_0^\infty \exp \left(g(x)\right) dx \approx \int_0^\infty \exp \left( n \ln (n) -\frac{(x-n)^2}{2 n} \right) dx = \left(\frac{n}{e} \right)^n \int_0^\infty \exp \left( -\frac{(x-n)^2}{2 n} \right) dx\] |
For large \(n\) (\(n\gt3\))
| \[ \int_0^\infty \exp \left( -\frac{(x-n)^2}{2 n} \right) dx \approx \int_{-\infty}^{+\infty} \exp \left( -\frac{x^2}{2 n} \right) dx = \sqrt{2\pi n}\] |
A slightly improved approximation for large \(n\) gives
| \[n!\approx\left(\frac{n}{e}\right)^n\sqrt{2\pi n} \left(1+\frac{1}{12n}\right)\] |
© J. Carstensen (Math for MS)